Закон движения частицы - это зависимость координат от времени.
Для проекций на ось координат ОХ можно записать:
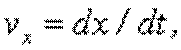 , ,
| (2.3) |
dx- проекция вектора перемещения 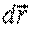 на ось х,
на ось х,
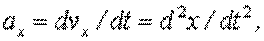
| (2.4) |
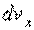 - проекция вектора приращения скорости
- проекция вектора приращения скорости 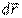 на ось х.
на ось х.
Аналогично определяются проекции скорости и ускорения на оси y и z
Модуль вектора скорости определяется формулой
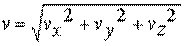 ,
,
а направление вектора 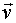 задается направляющими косинyсами по формулам:
задается направляющими косинyсами по формулам:
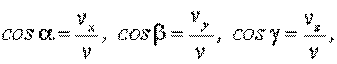
| (2.5) |
где α, β ,γ - углы между вектором 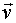 и осями х, у, z соответственно.
и осями х, у, z соответственно.
 .
.
Аналогично для ускорения 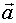 .
.
Естественный способ.
Его применяют, когда заранееизвестна траектория частицы.
Выбирается дуговая координата l – расстояние вдоль траектории от выбранного начала отсчета точки О (рис. 2.3).
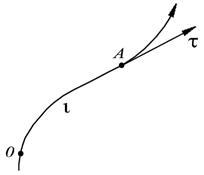
| Рис. 2.3. Естественный способ описания движения |
Тогда скорость.
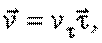
| (2.6) |
где 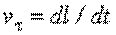 - проекция вектора
- проекция вектора 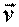 на направление вектора
на направление вектора 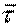 , причем
, причем 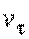 - величина алгебраическая. Кроме того
- величина алгебраическая. Кроме того 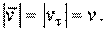
Ускорение. Продифференцируем (2.6) по времени:
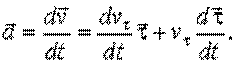
Последнее слагаемое этого выражения:
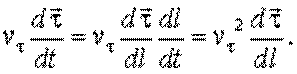
| (2.7) |
Рассмотрим приращение вектора 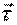 на участке dl(рис. 2.4).
на участке dl(рис. 2.4).
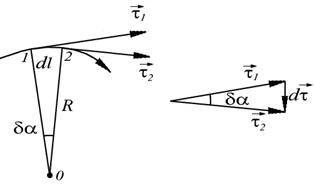 Рис. 2.4. Определение радиуса кривизны траектории
Рис. 2.4. Определение радиуса кривизны траектории
|
Как видно из рис. 2.4, угол 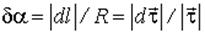 , откуда
, откуда 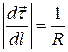 ,
,
причем при 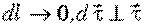 .
.
Если ввести единичный вектор нормали 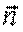 к траектории в точке 1, направленный к центру кривизны, то:
к траектории в точке 1, направленный к центру кривизны, то:
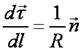
| (2.8) |
Подставляя (2.8) в (2.7), а затем полученное выражение - в (2.6), получим для вектора ускорения 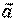

| (2.9) |
Здесь первое слагаемое называют тангенциальнымускорением, а второе - нормальным (центростремительным).
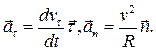
| (2.10) |
Тангенциальное ускорение показывает, как изменяется величина скорости, а нормальное – как изменяется ее направление.
Вращательное движение с постоянной скоростью означает отсутствие тангенциального ускорения и наличие только нормального.
В итоге полное ускорение 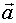 может быть представлено как сумма тангенциального
может быть представлено как сумма тангенциального 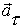 и нормального
и нормального 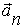 ускорений.
ускорений.
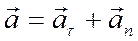
Модуль полного ускорения вычисляется по теореме Пифагора
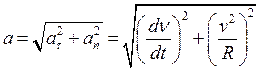
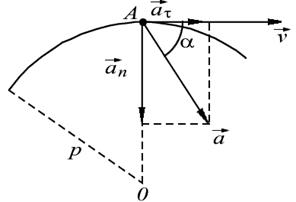
| Рис. 2.5. Определение полного ускорения частицы |
Из рис. 2.5 видно, что 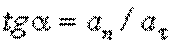
Дата добавления: 2017-06-02; просмотров: 2801;
