Интервал между событиями и собственные параметры частиц
Начальным элементом кинематики является элементарное перемещение точки, определяемое тройкой величин 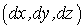 , геометрические свойства которой обуславливают свойства многих последующих звеньев цепочки. Свойства эти заключаются в том, что при повороте осей декартовой системы координат, величины
, геометрические свойства которой обуславливают свойства многих последующих звеньев цепочки. Свойства эти заключаются в том, что при повороте осей декартовой системы координат, величины 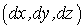 переходят в новую тройку
переходят в новую тройку 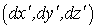 по правилу преобразования координат точек пространства - как проекции направленного отрезка. Если для удобства записи обозначить
по правилу преобразования координат точек пространства - как проекции направленного отрезка. Если для удобства записи обозначить 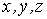 через
через 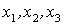 , то правило преобразования координат при повороте осей дается таблицей
, то правило преобразования координат при повороте осей дается таблицей
| X1 | X2 | X3 | |
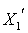
| 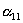
| 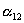
| 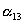
|
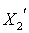
| 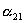
| 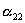
| 
|
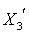
| 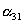
| 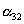
| 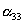
|
где штрихами обозначены новые (после поворота осей) координаты, а 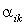 -косинусы углов между осями: i-й новой и k-ой старой (до поворота),
-косинусы углов между осями: i-й новой и k-ой старой (до поворота), 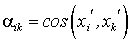 .
.
Пользуясь таблицей, легко выразить новые значения координат через старые и наоборот:
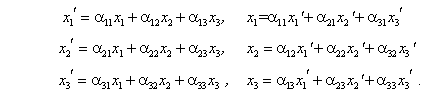
| (1.9) |
Сокращенно эти формулы записываются в виде (для i=1,2,3 и k=1,2,3)
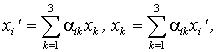
или, в предложенном Эйнштейном виде:
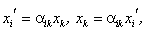
где опускается знак суммирования 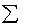 и принимается условие: по индексу, который повторяется, берется сумма, то есть i,k = 1,2,3.
и принимается условие: по индексу, который повторяется, берется сумма, то есть i,k = 1,2,3.
Учитывая, что такой же закон преобразования (1.9) сохраняется и для многих последующих звеньев логической цепочки (для перемещения, скорости, ускорения, силы, количества движения и пр.), в физике вводят понятие трехмерного вектора.
Всякая трехкомпонентная физическая величина ( ), составляющие которой преобразуются при повороте декартовых осей так же, как декартовы координаты точек, называется трехмерным вектором и обозначается одной буквой со стрелкой над ней: или просто (сокращенно: 3-вектор).
В соответствии с приведенным определением, компоненты 3-векторов 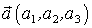 классической механики преобразуются при повороте осей декартовой системы координат по формулам
классической механики преобразуются при повороте осей декартовой системы координат по формулам
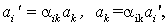 , ,
| (1.10) |
где 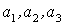 - компоненты до поворота осей, а
- компоненты до поворота осей, а  - после.
- после.
Логическая цепочка, на основе которой строится ньютонова механика состоит из нескольких частей. В самом начале на основе изменения радиус-вектора точки 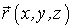 вводится элементарное ее перемещение
вводится элементарное ее перемещение 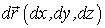 ; вслед за ним - скорость
; вслед за ним - скорость 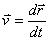 , т.е. вектор
, т.е. вектор 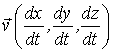 , затем ускорение
, затем ускорение 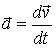 , вектор
, вектор 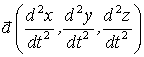 .
.
Теперь необходимо пройти такой же путь, насколько это возможно, на новой логической основе, опираясь на постулаты Эйнштейна и вытекающие из них преобразования Лоренца. Нужно будет обобщить как сами физические величины, так и связи между ними с учетом достигнутого уровня современной экспериментальной физики.
Ньютонова механика строится на известных представлениях о свойствах пространства и времени. Важнейшее из них - инвариантность расстояний между точками пространства при повороте осей декартовой системы, 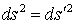 (в развернутом виде это равенство имеет вид
(в развернутом виде это равенство имеет вид 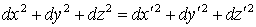 ) и также инвариантность времени,
) и также инвариантность времени, 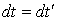 (выполняется во всех системах отсчета). Эти инварианты свойственны также и переходу I® II как при
(выполняется во всех системах отсчета). Эти инварианты свойственны также и переходу I® II как при 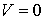 , так и при
, так и при 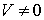 , что означает сохранение длины трехмерного вектора перемещения и интервала времени между событиями.
, что означает сохранение длины трехмерного вектора перемещения и интервала времени между событиями.
В теории относительности оба эти инварианта также имеют место, но лишь при параллельном сдвиге и повороте осей системы отсчета; они не выполняются при переходе I® II , когда система II движется относительно I.Однако, как оказалось, из преобразований Лоренца следует инвариантность некоторой комбинированной пространственно-временной физической величины при переходе от инерциальной системы отсчета I к равномерно движущейся относительно нее системе II. Упомянутая величина называется интервалом между двумя событиями. Преобразования Лоренца и интервал играют определяющую роль в отношении свойств пространства и времени в СТО.
Пусть в некоторой инерциальной системе отсчета I произошли два события 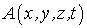 и
и 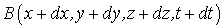 .
.
Дата добавления: 2017-06-02; просмотров: 456;
