Дифференциальные уравнения плоскопараллельного движения твердого тела

Свободное твердое тело будет совершать плоскопараллельное движение, если в нем существует плоское сечение, относительно которого масса тела распределена симметрично; силы, действующие на тело, расположены в плоскости этого сечения, а начальные скорости всех точек тела расположены в плоскостях, параллельных плоскости сечения. Движение тела может быть плоскопараллельным также и в силу наложенных на него связей, но это уже будет несвободное движение.

В кинематике было установлено, что положение твердого тела, совершающего плоскопараллельное движение, определяется тремя параметрами. За эти параметры выберем координаты центра масс тела и угол поворота тела относительно оси, перпендикулярной к рассматриваемому плоскому сечению тела.

Пусть система координат 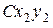, имеющая начало в центре масс тела, движется поступательно относительно неподвижной системы координат 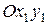. Положение тела будет полностью определено, если известны координаты центра масс ( 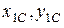) и угол 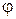между осью 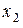и осью 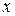системы координат 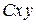, жестко связанной с телом (рис. *.12).

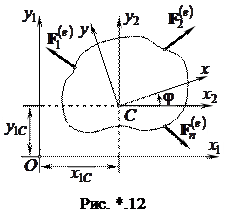В соответствии с теоремой о движении центра масс получаем зависимости, связывающие координаты центра масс тела и проекции главного вектора всех внешних сил ( 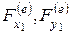), приложенных к твердому телу:

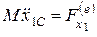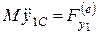, , (*.38)

где 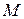– масса тела.

Используя теперь теорему об изменении кинетического момента в относительном движении по отношению к центру масс (можно показать, что она записывется также как и теорема об измененении кинетического момента относительно неподвижного центра), получим зависимость между углом поворота тела и силами, действующими на тело.

Так как в системе координат 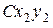твердое тело совершает вращательное движение вокруг оси, проходящей через центр масс перпендикулярно к плоскости движения тела, то кинетический момент тела относительно этой оси в соответствии с ранее полученной формулой будет равен 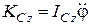. Следовательно, на основании последнего уравнения теоремы об изменении кинетического момента в относительном движении по отношению к центру масс имеем

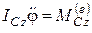, (*.39)

где 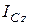– момент инерции тела относительно оси, перпендикулярной к плоскости движения тела и проходящей через центр масс тела;

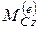– главный момент внешних сил всех внешних сил относительно той же самой оси.

Уравнения (*.38), (*.39) дают возможность решать задачи динамики плоскопараллельного движения твердого тела.

Указанные уравнения позволяют:

1) по заданным уравнениям движения тела 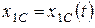, , 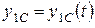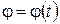его массе 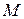и моменту инерции 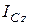определить главный вектор и главный момент внешних сил, действующих на тело (первая задача динамики);

2) по заданным внешним силам, приложенным к телу, начальным условиям 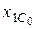, , 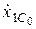, , 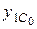, , 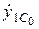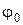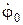по массе 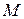и моменту инерции тела 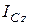найти уравнение плоскопараллельного движения тела (вторая задача динамики)

, , .

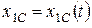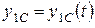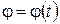Если тело совершает несвободное движение, то в число действующих сил следует включить реакции связей. Уравнения движения в этом случае будут

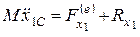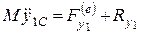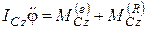, , , (*.40)

где 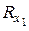, 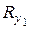– суммы проекций всех реакций соответственно на оси , ;

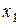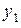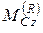– сумма моментов всех реакций относительно центра масс.

К уравнениям (*.40) следует еще добавить уравнения связей.