III. Линейность неопределенного интеграла.
Теорема 1. Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от слагаемых:
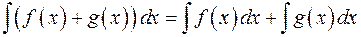
Теорема 2. Постоянный множитель можно выносить за знак неопределенного интеграла: 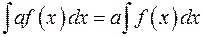 , где
, где 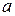 – постоянная.
– постоянная.
Совокупность теорем 1,2 называется свойством линейности неопределенного интеграла.
Пусть 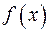 и
и 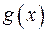 – функции,
– функции, 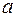 и
и 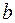 – числа. Тогда функция
– числа. Тогда функция 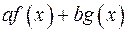 называется линейной комбинацией
называется линейной комбинацией 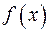 и
и 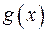 c числами
c числами 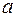 и
и 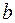 . Из теорем 1 и 2 следует, что неопределенный интеграл от линейной комбинации данных функций с данными числами равен линейной комбинации неопределенных интегралов от этих функций с теми же числами:
. Из теорем 1 и 2 следует, что неопределенный интеграл от линейной комбинации данных функций с данными числами равен линейной комбинации неопределенных интегралов от этих функций с теми же числами:
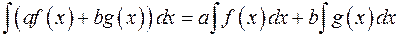 .
.
Понятие линейной комбинации распространяется на любое конечное число функций. Для случая 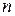 функций
функций 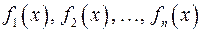 и
и 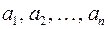 будем иметь:
будем иметь:
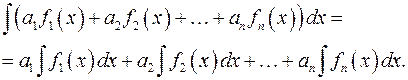
IV. Основные методы интегрирования.
Непосредственное интегрирование.
Таблица простейших интегралов.
1. 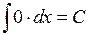
| 2. 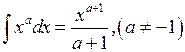
|
3. 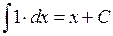
| 4. 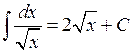
|
5. 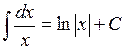
| 6. 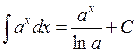
|
7. 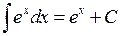
| 8. 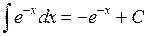
|
9. 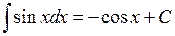
| 10. 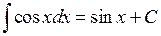
|
11. 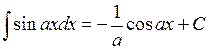
| 12. 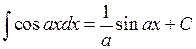
|
13. 
| 14. 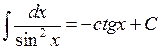
|
15. 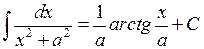
| 16. 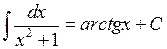
|
17. 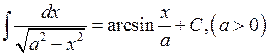
| 18. 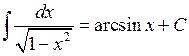
|
19. 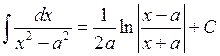
| 20. 
|
21. 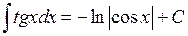
| 22. 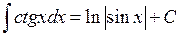
|
23. 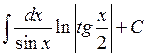
| 24. 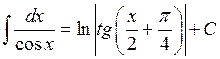
|
Доказательство любого из этих равенств сводится к определению неопределенного интеграла и к соответствующей формуле из таблицы производных.
Например, 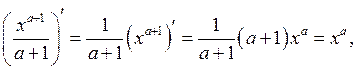 при
при 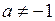 .
.
Значит, функция 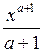 – первообразная для
– первообразная для 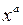 и согласно определению неопределенного интеграла:
и согласно определению неопределенного интеграла: 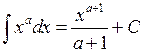 , при
, при 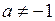 .
.
Приведем доказательство формулы 5 таблицы: 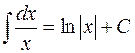 .
.
Согласно определению понятия модуля имеем, что
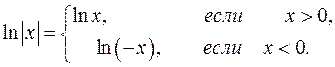
Значит 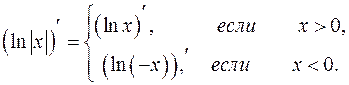
Для 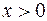
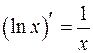 и согласно теореме о производной от сложной функции:
и согласно теореме о производной от сложной функции:
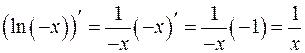
Таким образом, 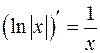 при всех
при всех 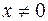 . Значит,
. Значит, 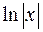 – первообразная для функции
– первообразная для функции 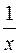 .
.
На основании определения неопределенного интеграла убеждаемся в справедливости формулы 5.
Примеры.
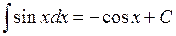 .
.

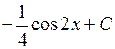 .
.
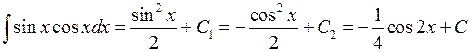
Первообразные 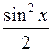 и
и 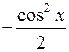 отличаются на постоянное слагаемое, так как
отличаются на постоянное слагаемое, так как
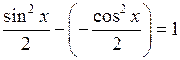 .
.
Процесс отыскания неопределенного интеграла от функции 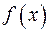 с использованием таблицы первообразных называется непосредственным интегрированием этой функции.
с использованием таблицы первообразных называется непосредственным интегрированием этой функции.
Дата добавления: 2019-07-26; просмотров: 1194;
