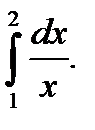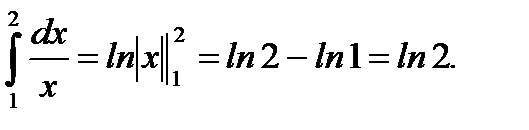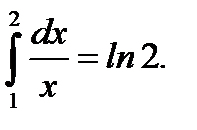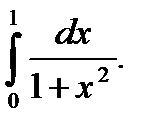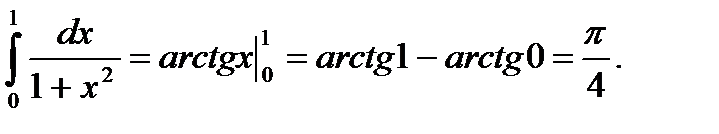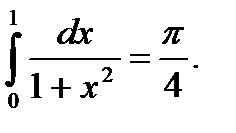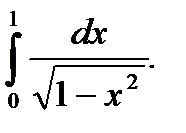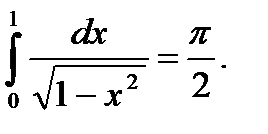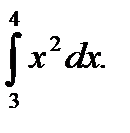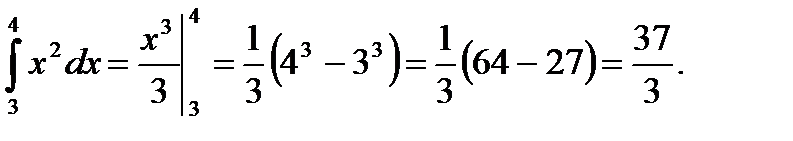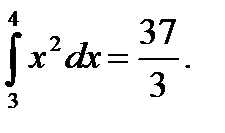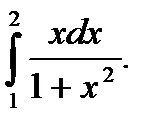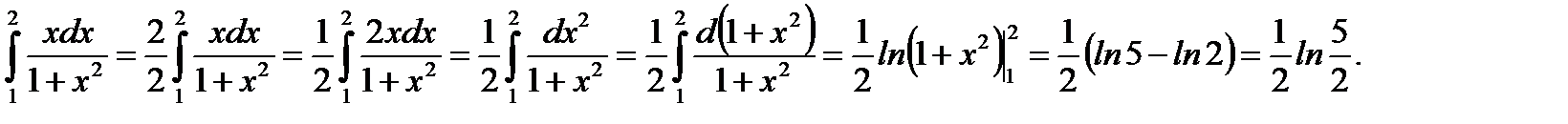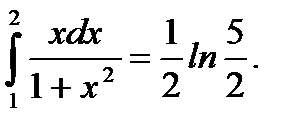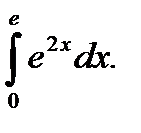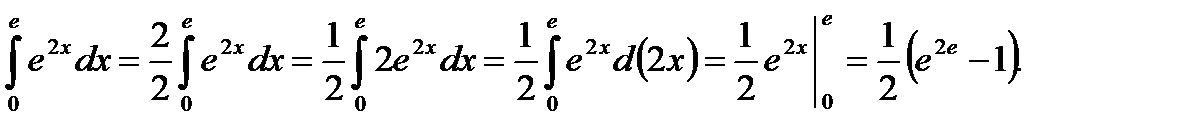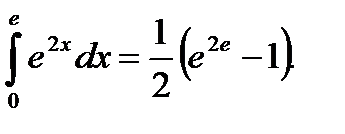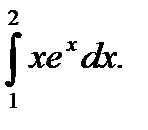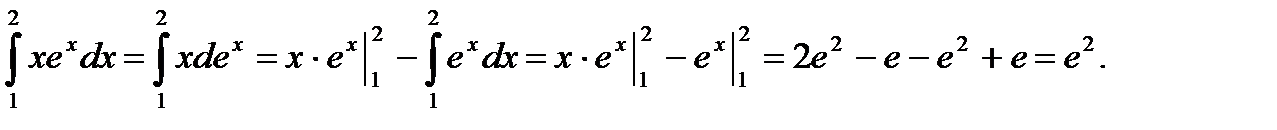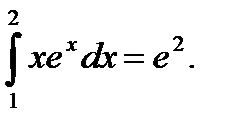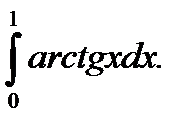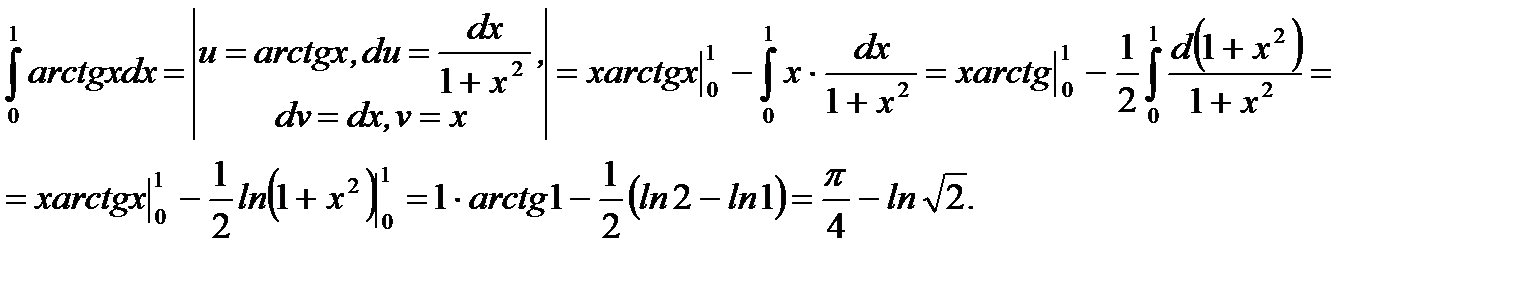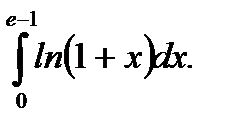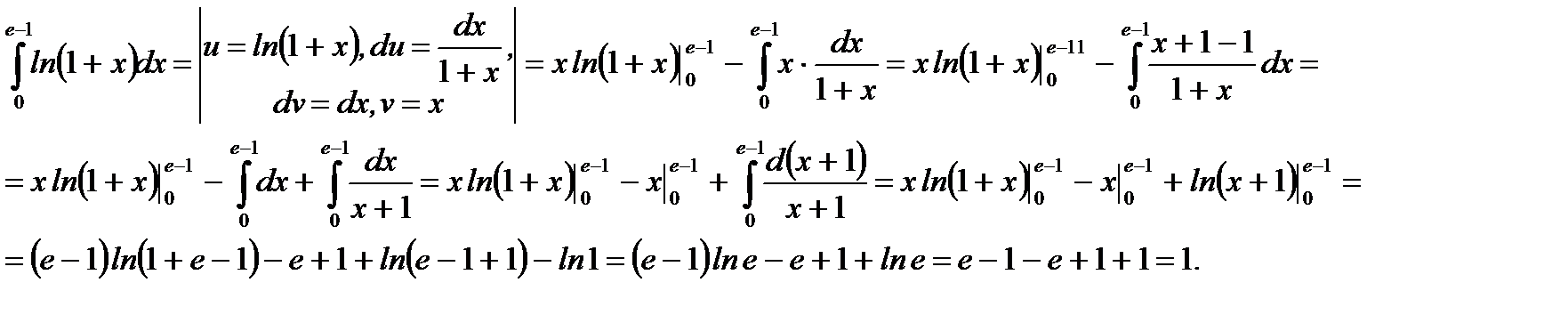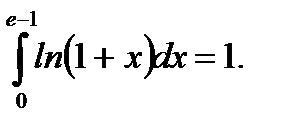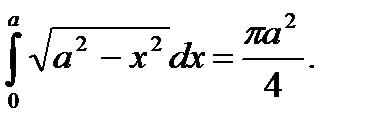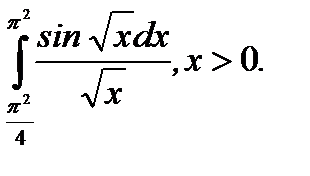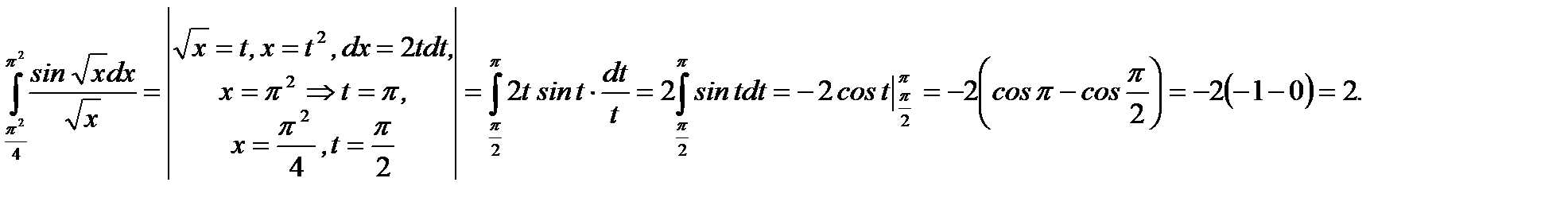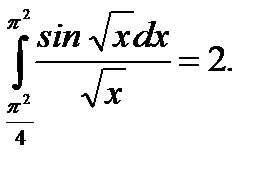Определение и вычисление определенного интеграла.
Рассмотрим геометрическую задачу вычисления площади криволинейной трапеции и покажем, как при ее решении приходим к понятию определенного интеграла.
Пусть на плоскости 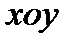 имеем криволинейную трапецию
имеем криволинейную трапецию 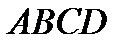 , ограниченную кривой
, ограниченную кривой 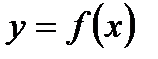 (функция
(функция 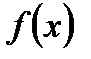 определена и непрерывна при
определена и непрерывна при  ) и двумя прямыми
) и двумя прямыми 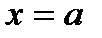 и
и  (см. рис. 5.1).
(см. рис. 5.1).
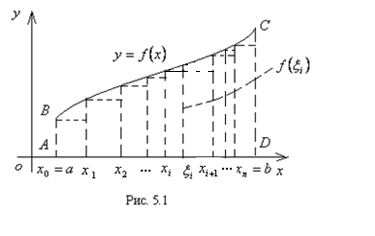
Разделим основание AD этой трапеции произвольным образом на 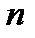 частей (разбиение Т) и проведем ординаты соответствующих точек деления
частей (разбиение Т) и проведем ординаты соответствующих точек деления

Отметим, что эти точки деления 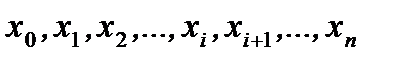 называются точками разбиения T. Возьмем
называются точками разбиения T. Возьмем 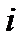 - тую элементарную трапецию и заменим ее приближенно прямоугольником с основанием
- тую элементарную трапецию и заменим ее приближенно прямоугольником с основанием 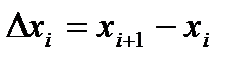 и высотой
и высотой 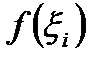 , где
, где 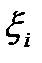 есть абсцисса произвольной точки из сегмента
есть абсцисса произвольной точки из сегмента 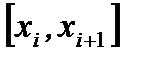 . Тогда площадь
. Тогда площадь 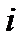 - той трапеции приближенно равна площади
- той трапеции приближенно равна площади 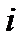 - го прямоугольника, т.е.
- го прямоугольника, т.е. 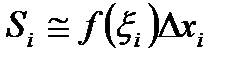 . Если суммировать площади всех элементарных прямоугольников
. Если суммировать площади всех элементарных прямоугольников 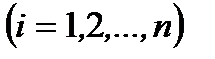 , то получим приближенную площадь криволинейной трапеции ABCD в виде
, то получим приближенную площадь криволинейной трапеции ABCD в виде
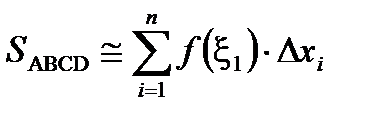
(5.35)
Очевидно, что точное значение криволинейной площади 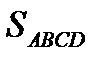 получим, если в (5.35) перейдем к пределу, когда max
получим, если в (5.35) перейдем к пределу, когда max 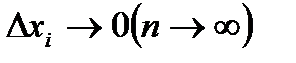 , т.е.
, т.е.
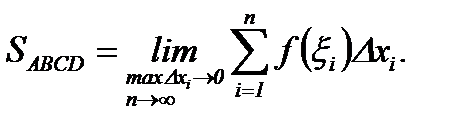 (5.36)
(5.36)
Конечный предел (5.36) называется определенным интегралом и обозначается так:
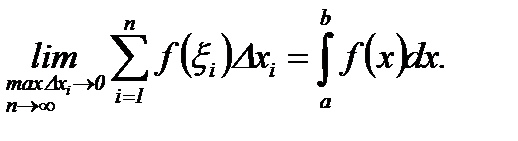 (5.37)
(5.37)
Определенный интеграл (5.37) вычисляем, основываясь на теорему Ньютона-Лейбница. Согласно этой теореме имеем
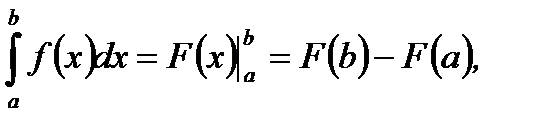 (5.38)
(5.38)
где 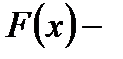 одна из первообразных функции
одна из первообразных функции 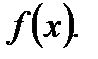
Ниже приведем некоторые основные свойства определенного интеграла:
1. Определенный интеграл от интегрируемой функции 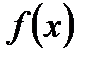 в пределах от
в пределах от  до
до 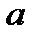 равен нулю, т.е.
равен нулю, т.е.
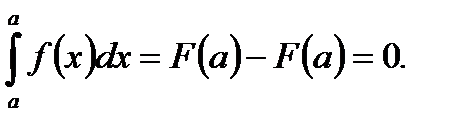 (5.39)
(5.39)
2. При перестановке пределов интегрирования в определенном интеграле знак интеграла меняется на обратное, т.е. если 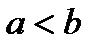 и
и 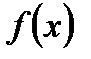 интегрируема на сегменте
интегрируема на сегменте 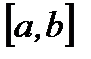 , то
, то
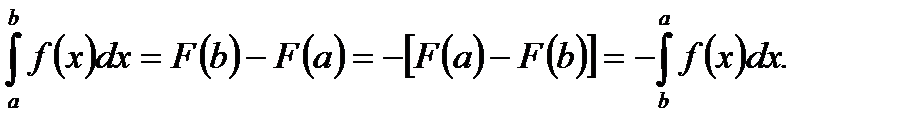 . (5.40)
. (5.40)
3. Если функции 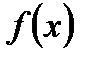 и
и 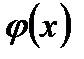 интегрируемы на сегменте
интегрируемы на сегменте 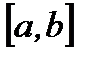 , то функции
, то функции 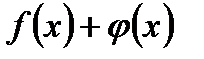 и
и 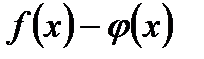 также интегрируемы на сегменте
также интегрируемы на сегменте 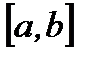 и
и
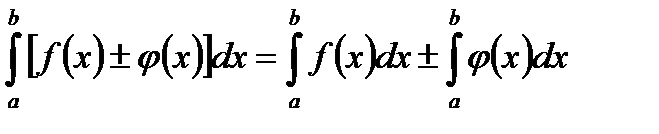 . (5.41)
. (5.41)
4. Если функция 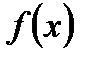 интегрируема на сегменте
интегрируема на сегменте 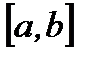 , то
, то 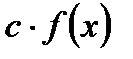 , где
, где 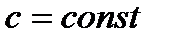 , также интегрируема на сегменте
, также интегрируема на сегменте 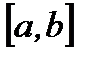 и
и
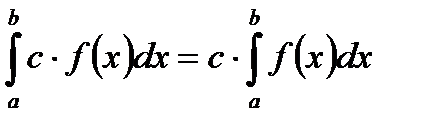 . (5.42)
. (5.42)
5. Если функция 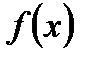 интегрируема на сегментах
интегрируема на сегментах 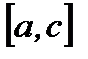 и
и 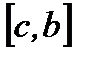 , где
, где 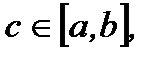 то она интегрируема и на сегменте
то она интегрируема и на сегменте  , причем
, причем
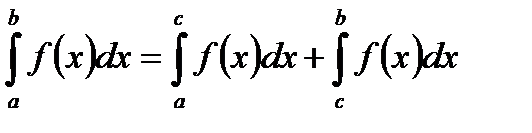 . (5.43)
. (5.43)
6. Если функция 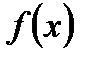 интегрируема на сегменте
интегрируема на сегменте 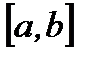 , то
, то 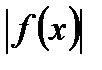 также интегрируема на этом сегменте и справедливо неравенство
также интегрируема на этом сегменте и справедливо неравенство
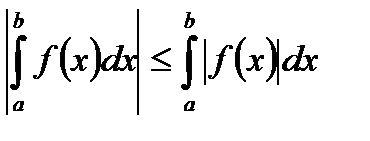 . (5.44)
. (5.44)
7. Если функции 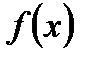 и
и 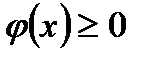 интегрируемы на сегменте
интегрируемы на сегменте 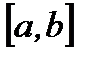 и
и 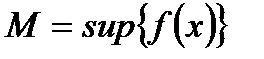 ,
, 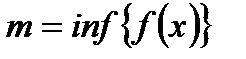 на этом сегменте, то справедливы неравенства
на этом сегменте, то справедливы неравенства
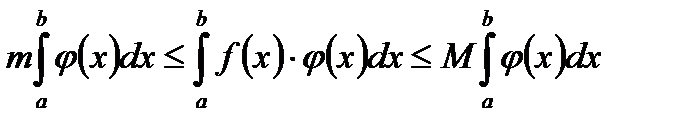 . (5.45)
. (5.45)
Заметим, что если при вычислении определенного интеграла 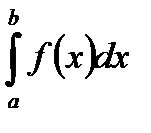 производим замену переменной
производим замену переменной 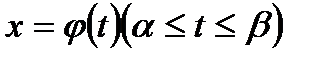 , то пределы интегрирования меняются и имеем
, то пределы интегрирования меняются и имеем
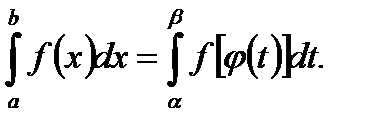 (5.46)
(5.46)
Отметим также, что формула интегрирования по частям для определенного интеграла имеет вид
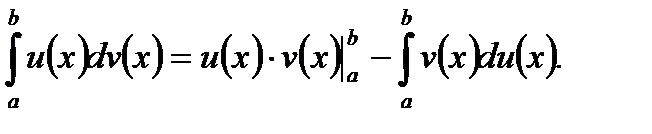 (5.47)
(5.47)
Пример 5.34.Вычислить определенный интеграл 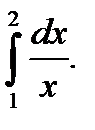
Решение.
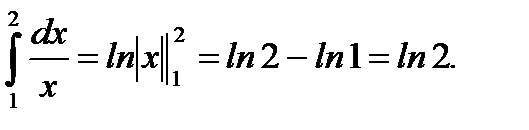
Ответ: 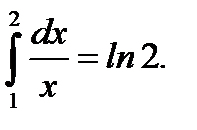
Пример 5.35.Вычислить определенный интеграл 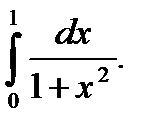
Решение.
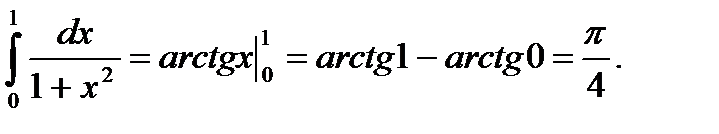
Ответ: 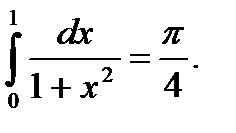
Пример 5.36.Вычислить определенный интеграл 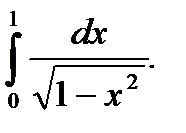
Решение.

Ответ: 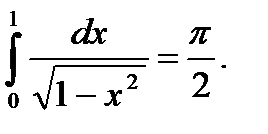
Пример 5.37.Вычислить определенный интеграл 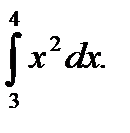
Решение.
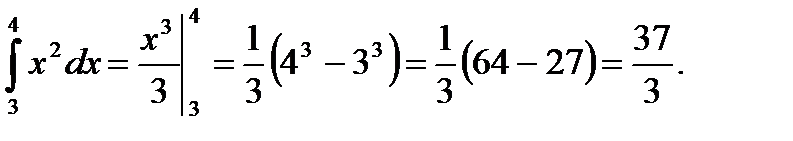
Ответ: 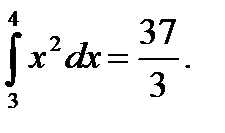
Пример 5.38.Вычислить определенный интеграл 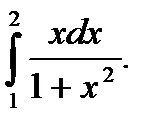
Решение.
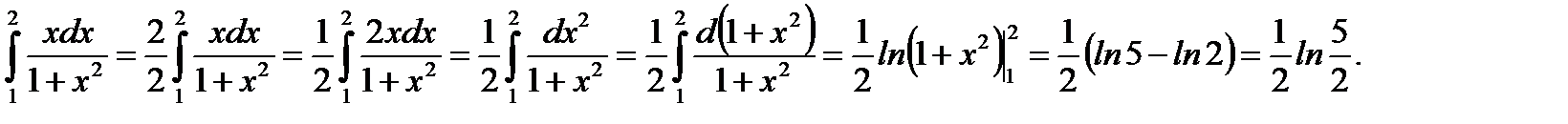
Ответ: 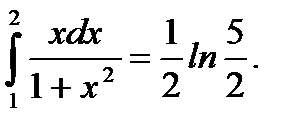
Пример 5.39.Вычислить определенный интеграл 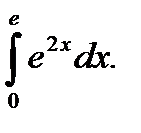
Решение.
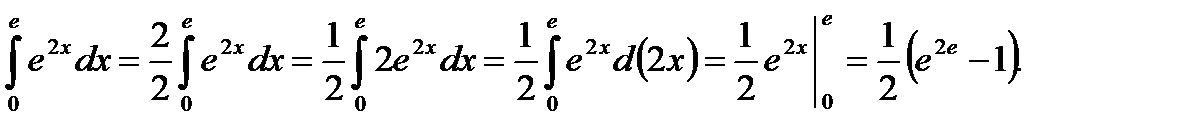
Ответ: 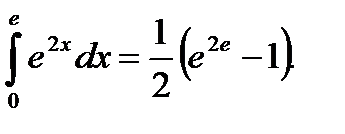
Пример 5.40.Вычислить определенный интеграл 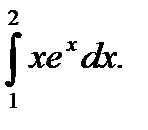
Решение.
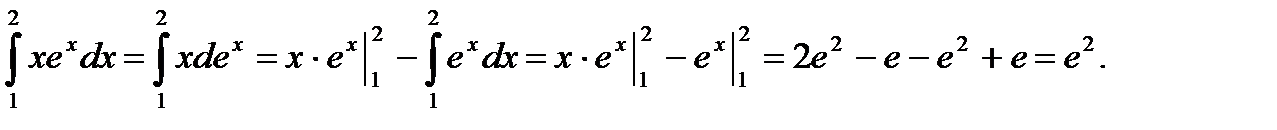
Ответ: 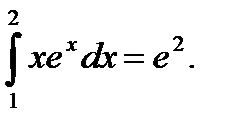
Пример 5.41.Вычислить определенный интеграл 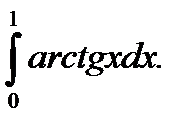
Решение.
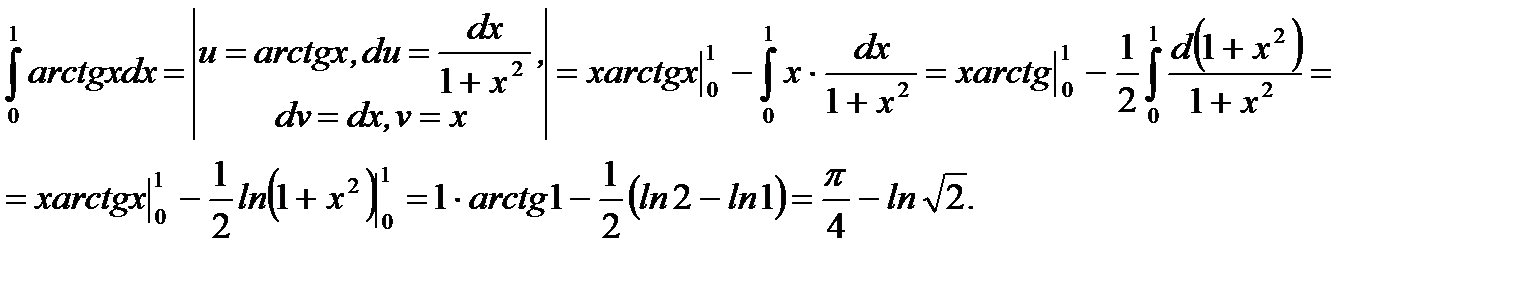
Ответ: 
Пример 5.42.Вычислить определенный интеграл 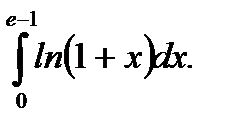
Решение.
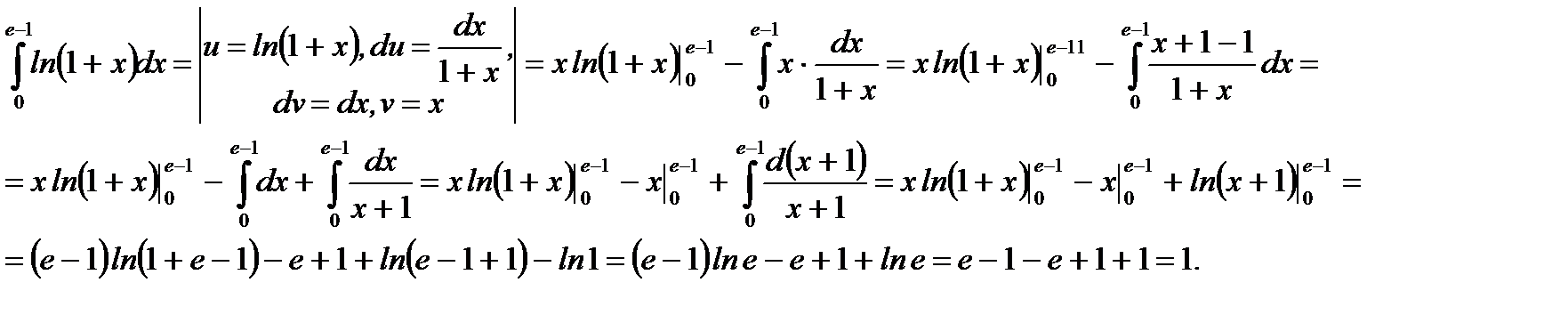
Ответ: 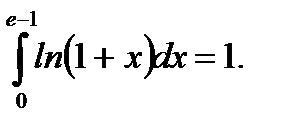
Пример 5.43.Вычислить определенный интеграл 
Решение.
Ответ: 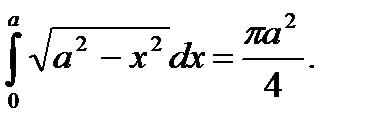
Пример 5.44.Вычислить определенный интеграл 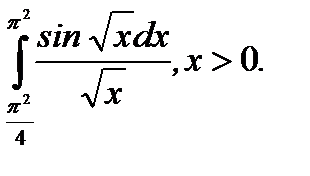
Решение.
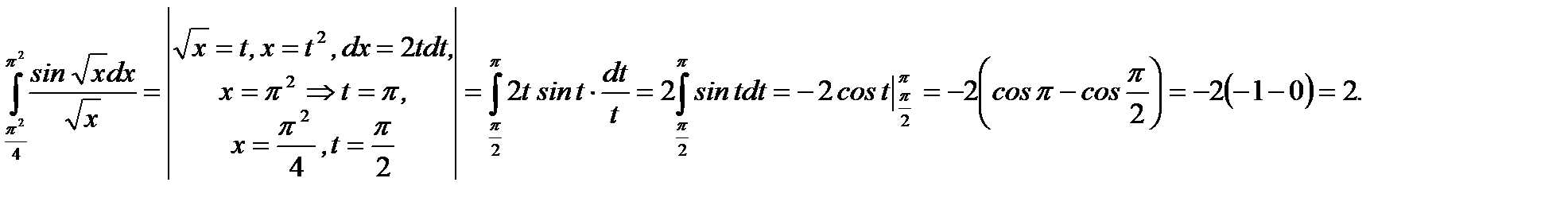
Ответ: 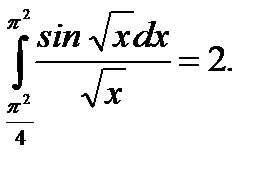
Дата добавления: 2018-11-25; просмотров: 579;
 имеем криволинейную трапецию
имеем криволинейную трапецию 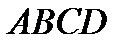 , ограниченную кривой
, ограниченную кривой 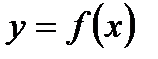 (функция
(функция 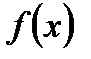 определена и непрерывна при
определена и непрерывна при  ) и двумя прямыми
) и двумя прямыми 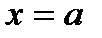 и
и  (см. рис. 5.1).
(см. рис. 5.1).
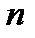 частей (разбиение Т) и проведем ординаты соответствующих точек деления
частей (разбиение Т) и проведем ординаты соответствующих точек деления
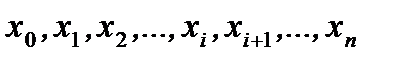 называются точками разбиения T. Возьмем
называются точками разбиения T. Возьмем 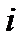 - тую элементарную трапецию и заменим ее приближенно прямоугольником с основанием
- тую элементарную трапецию и заменим ее приближенно прямоугольником с основанием 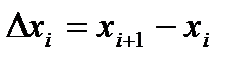 и высотой
и высотой 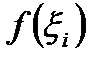 , где
, где 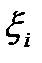 есть абсцисса произвольной точки из сегмента
есть абсцисса произвольной точки из сегмента 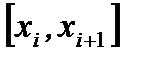 . Тогда площадь
. Тогда площадь 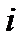 - той трапеции приближенно равна площади
- той трапеции приближенно равна площади 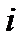 - го прямоугольника, т.е.
- го прямоугольника, т.е. 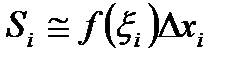 . Если суммировать площади всех элементарных прямоугольников
. Если суммировать площади всех элементарных прямоугольников 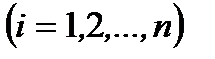 , то получим приближенную площадь криволинейной трапеции ABCD в виде
, то получим приближенную площадь криволинейной трапеции ABCD в виде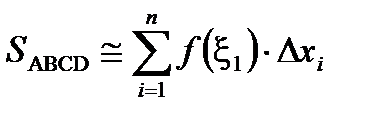
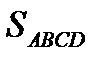 получим, если в (5.35) перейдем к пределу, когда max
получим, если в (5.35) перейдем к пределу, когда max 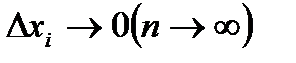 , т.е.
, т.е.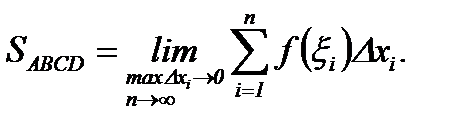 (5.36)
(5.36)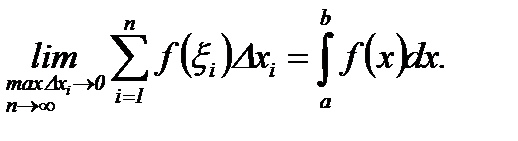 (5.37)
(5.37)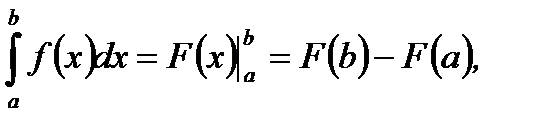 (5.38)
(5.38)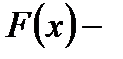 одна из первообразных функции
одна из первообразных функции 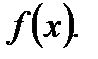
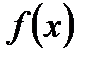 в пределах от
в пределах от  до
до 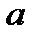 равен нулю, т.е.
равен нулю, т.е.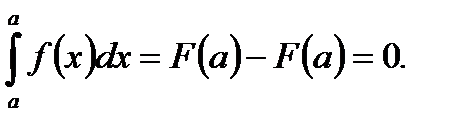 (5.39)
(5.39)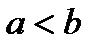 и
и 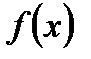 интегрируема на сегменте
интегрируема на сегменте 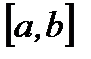 , то
, то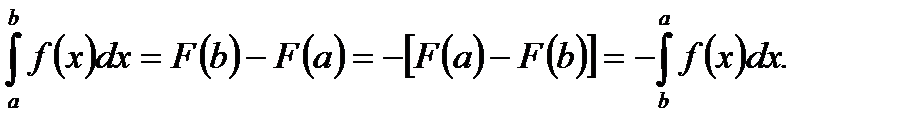 . (5.40)
. (5.40)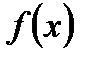 и
и 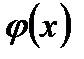 интегрируемы на сегменте
интегрируемы на сегменте 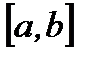 , то функции
, то функции 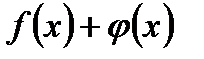 и
и 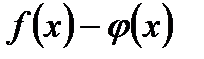 также интегрируемы на сегменте
также интегрируемы на сегменте 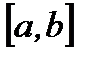 и
и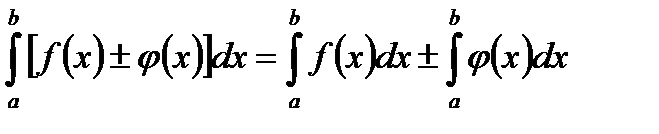 . (5.41)
. (5.41)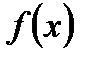 интегрируема на сегменте
интегрируема на сегменте 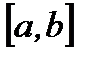 , то
, то 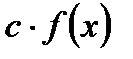 , где
, где 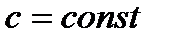 , также интегрируема на сегменте
, также интегрируема на сегменте 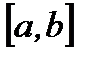 и
и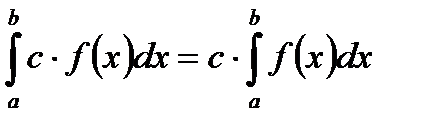 . (5.42)
. (5.42)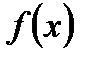 интегрируема на сегментах
интегрируема на сегментах 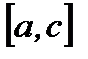 и
и 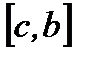 , где
, где 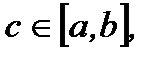 то она интегрируема и на сегменте
то она интегрируема и на сегменте  , причем
, причем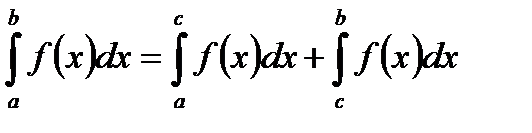 . (5.43)
. (5.43)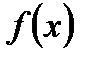 интегрируема на сегменте
интегрируема на сегменте 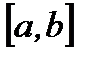 , то
, то 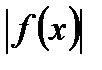 также интегрируема на этом сегменте и справедливо неравенство
также интегрируема на этом сегменте и справедливо неравенство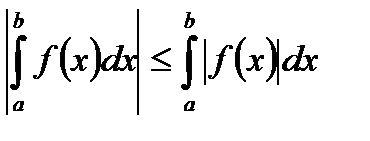 . (5.44)
. (5.44)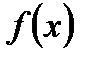 и
и 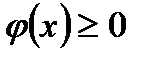 интегрируемы на сегменте
интегрируемы на сегменте 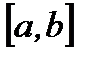 и
и 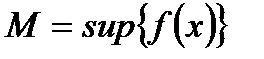 ,
, 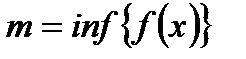 на этом сегменте, то справедливы неравенства
на этом сегменте, то справедливы неравенства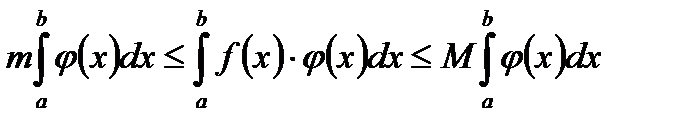 . (5.45)
. (5.45)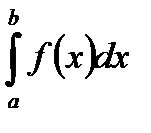 производим замену переменной
производим замену переменной 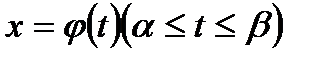 , то пределы интегрирования меняются и имеем
, то пределы интегрирования меняются и имеем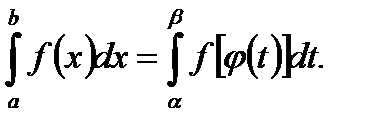 (5.46)
(5.46)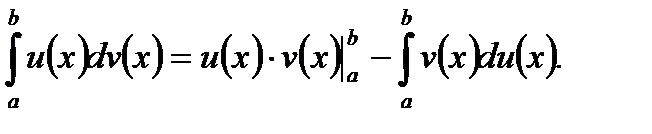 (5.47)
(5.47)