Второго порядка и свойства их решений

Многие задачи физики, механики и техники приводят к дифференциальным уравнениям в частных производных второго порядка, причем линейных относительно искомой функции и ее частных производных.

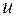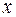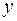Общий вид линейного дифференциального уравнения второго порядка при условии, что функция зависит от двух переменных и , таков:

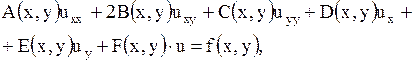
(1.88)

где 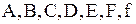- данные непрерывные функции, определяемые в некоторой области 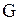переменных 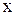и 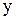, причем 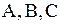имеют непрерывные частные производные до 2-го порядка включительно.

Чаще всего коэффициенты перед искомой функцией 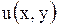и ее производными – числа.

Если в уравнении (1.88) 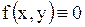, то уравнение называется однородным; если 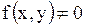, то уравнение называется неоднородным.

Обсудим особенность решений однородного уравнения

.

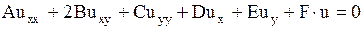(1.89)

Решения линейных однородных уравнений вида (1.89) обладают следующим свойством.

Если каждая из функций 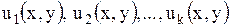является решением уравнения (1.89), то и их линейная комбинация

,

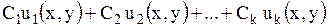(1.90)

где 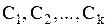- произвольные постоянные, также является решением этого уравнения.

Это утверждение легко проверить, подставив в уравнение (1.89) вместо 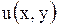выражение (1.90) и производные 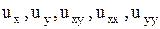указанной линейной комбинации.

Такое же свойство, как известно, имеет место для обыкновенных дифференциальных уравнений, но 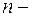го порядка.

Уравнение же в частных производных может иметь бесконечное множество линейно независимых частных решений, т.е. такое множество решений, любое конечное число которых является функциями линейно независимыми. (Напомним, система функций 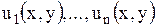называется линейно независимой, если ни одна из этих функций не является линейной комбинацией остальных). В соответствии с этим имеют дело с рядами, членами которых служат произведения произвольных постоянных на частные решения:

.

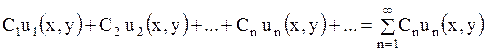(1.91)

Будем рассматривать только такие ряды, суммы которых есть непрерывные функции

.

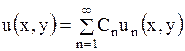Кроме того, будем предполагать, что эти ряды можно дважды почленно дифференцировать. При таких предположениях функция 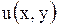, которая есть сумма ряда (1.91), так же как и члены ряда, является решением уравнения (1.89).