Метод Рунге-Кутта для уравнений первого порядка

Рассмотрим задачу Коши для дифференциального уравнения.

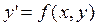
с начальным условием .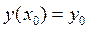

Обозначим через 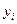приближенное значение искомого решения в точке 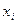. По методу Рунге-Кутта вычисление приближенного значения 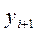в следующей точке 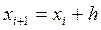производится по формулам

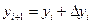
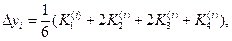
где

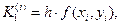
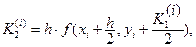
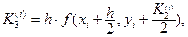
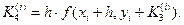
Для записи вычислений используется таблица Правило 4-го порядка точности.

Таблица 9.1.

Шаблон для вычисления решения уравнения (9.6) по методу Рунге-Кутта.

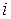
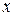
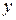
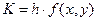
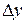
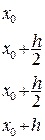
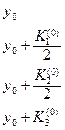
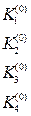
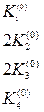
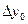
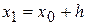
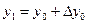
Пример 9.6. Используя метод Рунге–Кутта составить таблицу приближенных значений интеграла дифференциального уравнения 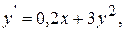удовлетворяющего начальным условиям y(0)=0.2 на отрезке [0;0.5] с шагом h=0.1. Все вычисления будем вести с четырьмя десятичными знаками, расположим их в таблице.

Таблица 9.2.

Решение примера методом Рунге-Кутта.

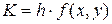
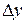
	0,05 0,05 0,1	0,2 0,206 0,2069 0,2138	0,012 0,0137 0,0138 0,0157	0,012 0,0274 0,0276 0,0157
				0,0138
	0,1 0,15 0,15 0,2	0,2138 0,2217 0,2227 0,2317	0,0157 0,0177 0,0179 0,0201	0,0157 0,0354 0,0358 0,0201
				0,0178
	0,2 0,25 0,25 0,3	0,2317 0,2417 0,2429 0,2544	0,0201 0,0225 0,0227 0,0254	0,0201 0,0250 0,0454 0,0254
				0,0227
	0,3 0,35 0,35 0,4	0,2544 0,267 0,2685 0,2829	0,0254 0,0284 0,0286 0,032	0,0254 0,0568 0,0572 0,032
				0,0286
	0,4 0,45 0,45 0,5	0,2829 0,2989 0,3008 0,3190	0,032 0,0358 0,0361 0,0405	0,032 0,0716 0,0722 0,0405
				0,0360
	0,5	0,3189

При решении задачи Коши для системы дифференциальных уравнений методом Рунге-Кутта

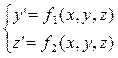
применим формулы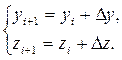

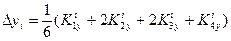
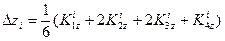
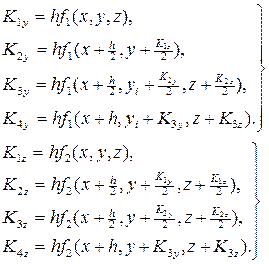
Для контроля правильности выбора шага h рекомендуется вычислять дробь 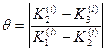. Величина q не должна превышать нескольких сотых. В противном случае шаг следует уменьшить.

Для определения точности пользуются двойным пересчетом.

,

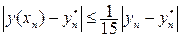где 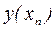- точное решение уравнения (9.6) в точке 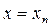, а y_n и 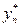приближенные значения, полученные при расчете с шагом h и с шагом 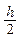, соответственно. Если y_n и 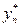мало различимы, то шаг выбран оптимально.

Для решения обыкновенных дифференциальных уравнений и систем в Mathcad предназначено несколько стандартных функций. В частности, для реализации метода Рунге-Кутта четвертого порядка существует функция rkfixed(y,a,b,n,D).

Параметры этой функции:

y-вектор начальных значений,

а,b- начало и конец промежутка интегрирования,

n-число интервалов, на которое делится промежуток интегрирования,

D-вектор правых частей системы обыкновенных дифференциальных уравнений.

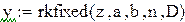
Применим данную функцию к решению примера 9.6.

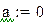
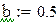
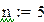
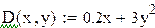
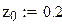
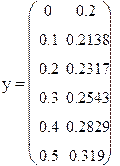
Рис 9.2 Решение примера 9.5 в Mathcad

Пример 9.6. Решим систему обыкновенных дифференциальных уравнений первого порядка 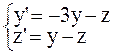с начальными условиями y(0)=2 , z(0)=-1

с помощью этой же стандартной функции на отрезке [0;0.5] с шагом h=0.1

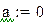
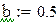
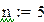
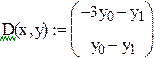
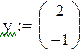
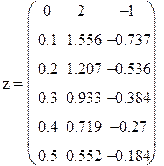
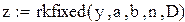
Рис 9.3. Решение примера 9.6 в Mathcad

Первый столбец таблицы это значения переменной x, второй столбец таблицы значения у, а третий столбец значения z в точках от ноля до 0,5 с шагом 0,1.

Пример 9.7. Решить задачу Коши для о.д.у. y"+3y'-xy-x³=5 y(0)=1 y'(0)=2 на отрезке [0;0.5] с шагом h=0.1

Решение уравнения более высокого порядка находится сведением уравнения к системе уравнений первого порядка и применением стандартной функции маткада rkfixed.

После замены переменных получаем систему

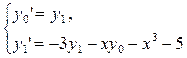
С начальными условиями y₀(0)=1 y₁(0)=2

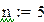
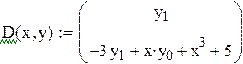
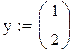
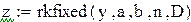
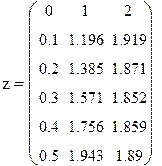
Решение уравнения- второй столбец таблицы.

Рис 9.4. Решение примера 9.7 в Mathcad

Список литературы

1. Демидович, Б.П. Основы вычислительной математики [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон. - Санкт-Петербург: Лань, 2009. - 672 с.

2. Копченова, Н. В. Вычислительная математика в примерах и задачах [Текст]: учеб. Пособие для студентов вузов/ Н. В. Копченова, И.А. Марон. - Санкт-Петербург: Лань, 2008. - 368 с.

3. Демидович, Б.П. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения [Текст]: учеб. Пособие для студентов вузов/ Б.П. Демидович, И.А Марон, Э.З. Шувалова. - Санкт-Петербург: Лань, 2010. - 400 с.

4. Бахвалов, Н.С. Численные методы [Текст]: учеб. Пособие для студентов вузов/ Н.С. Бахвалов, Н.П., Жидков, Г.М. Кобельков. М: Бином, 2003. - 632 с.

5. Поршнев, С.В. Численные методы на базе Mathcad [Текст]: учеб. Пособие для студентов вузов/ С.В. Поршнев, И.В. Беленкова.- Санкт-Петербург: БХВ-Петербург, 2005. - 464 с.

1. Кирьянов, Д. В. MathCAD 14[Текст]:/Д.В. Кирьянов - Санкт-Петербург: БХВ-Петербург, 2007. - 704 с.