Метод последовательных приближений.

Рассмотрим задачу Коши для дифференциального уравнения первого порядка

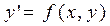
с начальным условием 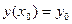. Решение этой задачи эквивалентно решению интегрального уравнения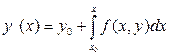

Метод последовательных приближений состоит в том, что решение 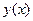получают как предел последовательности функций 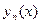, которые находятся по рекуррентной формуле

.

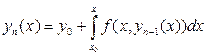Доказано, если правая часть 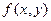в некотором замкнутом прямоугольнике 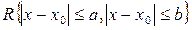удовлетворяет условию Липшица по y:

,

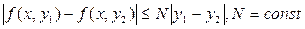то независимо от выбора начальной функции последовательные приближения 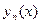сходятся на некотором отрезке 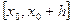к решению задачи Коши.

Если f(x,y) непрерывна в прямоугольнике R, то оценка погрешности дается неравенством

,

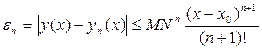где 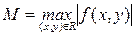, а число h определяется из условия

.

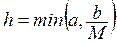В качестве начального приближения 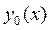можно взять любую функцию, достаточно близкую к точному решению.

Пример 9.3. Найти три последовательных приближения решения уравнения

y^'=x²+y² с начальным условием y(0)=0.

Учитывая начальное условие, заменяем уравнение интегральным

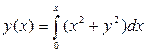
В качестве начального приближения возьмем y₀(x)≡0

Первое приближение находим по формуле

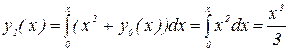
Аналогично получим второе и третье приближения:

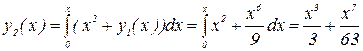
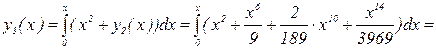
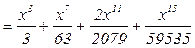
На практике количество приближений выбирают так, чтобы y_n и y_n-1 приближения совпадали в пределах допустимой точности. Для n=3 и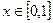

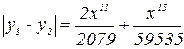y₃ вычислено с точностью порядка 0.001.