Закон больших чисел Чебышева.
ЗАКОНЫ БОЛЬШИХ ЧИСЕЛ.
Смысл закона больших чисел Чебышева состоит в следующем.
В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.
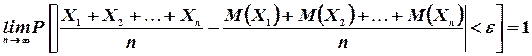
Частный случай закона больших чисел Чебышева можно сформулировать так.
Средняя арифметическая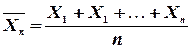 
попарно независимых случайных величин 
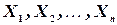, имеющих ограниченные в совокупности дисперсии и одинаковые математические ожидания 
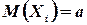, сходится по вероятности к а.
То есть, если число измерений достаточно велико, то с практической достоверностью можно утверждать, что каково бы ни было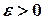 
, средняя арифметическая результатов измерений отличается от истинного значения аменьше, чем на 
.
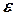Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.
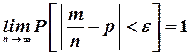
иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А).
Оглавление.
1. Леммы Чебышева.
2. Закон больших чисел Чебышева.
3. Частный случай закона больших чисел Чебышева.
4. Закон больших чисел Бернулли.
1. Леммы Чебышева.
В этом пункте докажем следующие две леммы, принадлежащие Чебышеву.
Лемма 1. Пусть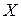 
— случайная величина, принимающая только неотрицательные значения; тогда
Доказательство:Для простоты докажем это утверждение для дискретной случайной величины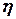 
, принимающей значения x1, x2, ..., xn, при условии 
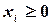. По аксиоме сложения вероятностей имеем
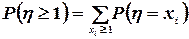
где суммирование распространено на все значения xi, большие или равные единице. Но для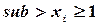 
, очевидно,
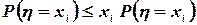
Поэтому
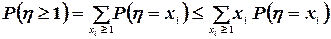(50)
где xi<1. Эта сумма неотрицательна, так как все 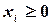по условию, а вероятности 
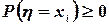. Поэтому
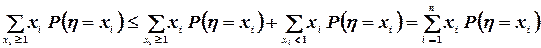(51)
Последняя сумма распространена на все значения xi, принимаемые случайной ветчиной 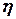. Но эта сумма по определению равна математическому ожиданию:
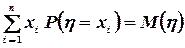
Сопоставляя соотношения (50) и (51), имеем
Тем самым лемма доказана.
Лемма 2. Пусть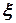 
— случайная величина, а 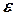- положительное число. Тогда вероятность того, что модуль отклонения случайной величины 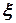от ее математического ожидания окажется меньше, чем 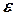, больше или равна разности
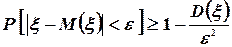(52)
Неравенство (52) называется неравенством Чебышева.
Доказательство: Рассмотрим сначала неравенство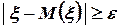 
. Так как оно равносильно неравенству 
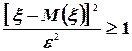то
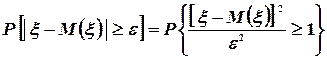
Случайная величина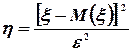 
неотрицательна и, значит, удовлетворяет условиям первой леммы Чебышева. Следовательно,
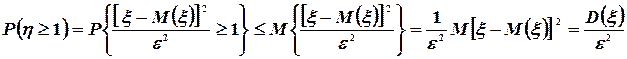
так как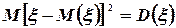 
.
Поэтому
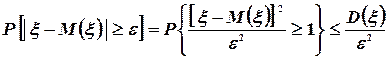(53)
Так как событие, выражаемое неравенством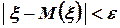 
, противоположно событию, выражаемому неравенством 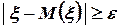, то
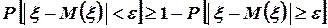
Принимая во внимание соотношение (53), окончательно получим
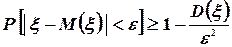
Закон больших чисел Чебышева.
Имеет место следующее утверждение.
Пусть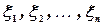 
- последовательность попарно независимых случайных величин, имеющих ограниченные в совокупности дисперсии, т. е. 
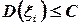для любого i. Тогда, каково бы ни было 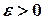, справедливо соотношение
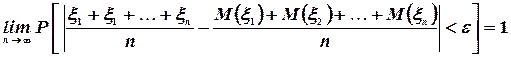(54)
Доказательство: Обозначим через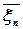 
величину 
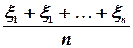, т.е. среднюю арифметическую n случайных величин. Случайная величина 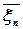имеет математическое ожидание
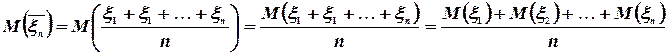
и дисперсию
(здесь мы воспользовались свойствами математического ожидания и дисперсии). Применяя к случайной величине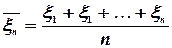 
вторую лемму Чебышева, найдем, что
т.е.
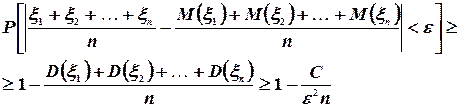
так как 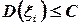при любом i и, следовательно,
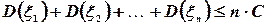
Учитывая, что вероятность любого события не превосходит единицы, получим
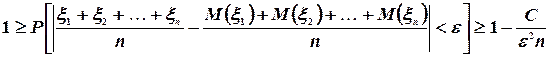
Переходя к пределу при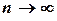 
, имеем
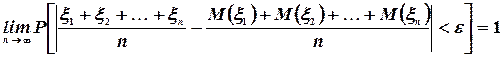
Смысл закона больших чисел Чебышева состоит в следующем.
В то время как отдельная случайная величина может принимать значения, очень далекие от своего математического ожидания, средняя арифметическая большого числа случайных величин с вероятностью, близкой к единице, принимает значение, мало отличающееся от среднего арифметического их математических ожиданий.
Дата добавления: 2018-11-25; просмотров: 293;