Общая формула трапеций и ее остаточный член
 |
Рис 8.1. Общая формула трапеций
Для вычисления интеграла 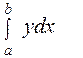 разделим промежуток интегрирования [a,b] на n равных частей
разделим промежуток интегрирования [a,b] на n равных частей 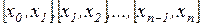 и к каждому из них применим формулу трапеций (8.4).
и к каждому из них применим формулу трапеций (8.4).
Положим 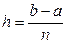 и обозначим через
и обозначим через 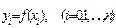 значения подынтегральной функции в точках xi тогда:
значения подынтегральной функции в точках xi тогда: 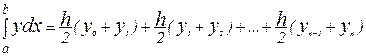 , или
, или
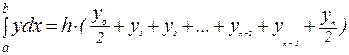 . (8.5)
. (8.5)
Геометрически формула (8.5) получается в результате замены графика подынтегральной функции 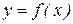 ломаной линией.
ломаной линией.
Oстаточный член общей формулы трапеций (8.5) равен:
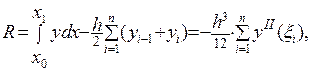 где
где 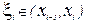 . (8.6)
. (8.6)
Рассмотрим среднее арифметическое значение второй производной 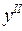 на отрезке [a,b] по всем промежуткам
на отрезке [a,b] по всем промежуткам
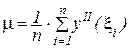 (8.7)
(8.7)
Очевидно, m заключается между наименьшим m2 и наибольшим M2 значениями второй производной 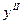 на отрезке [a,b], т.е.
на отрезке [a,b], т.е. 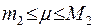 .
.
В силу непрерывности 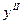 на отрезке [a,b], она принимает все значения от m2 до M2. Значит, существует точка ξ, такая что μ=f''(ξ). Из формул (8.6) и (8.7) получим:
на отрезке [a,b], она принимает все значения от m2 до M2. Значит, существует точка ξ, такая что μ=f''(ξ). Из формул (8.6) и (8.7) получим:
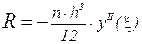 (8.8)
(8.8)
где 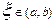
Пример 8.1. Выполнено в Mathcad
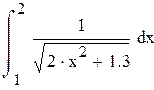
|
Вычислить интеграл
по методу трапеций с тремя десятичными знаками.
Сначала для сравнения покажем результат, вычисленный в Mathcad стандартным способом с тремя верными цифрами после запятой.
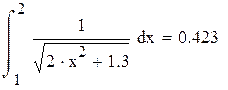
|
В Mathcad числа могут быть вычислены с 17 десятичными знаками, поэтому не будем учитывать погрешности вычислений и тогда погрешность метода ε=0,0005. Для достижения заданной точности решим неравенство
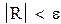
|
| находится по формуле |
| где R- остаточный член формулы трапеций, который находится по формуле (8.8) |
| Пусть M-максимальное по модулю значение f2(x) на [a,b] тогда |
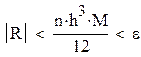
|
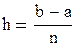
|
| так как |
Подставляем в формулу h и решаем неравенство относительно n:
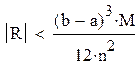
|
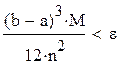
|
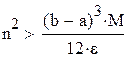
|
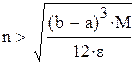
|
Для всех натуральных значений "n" больших , чем полученный корень, остаточный член формулы трапеций 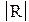 будет меньше заданной точности e будет меньше заданной точности e
|
| Hайдем вторую производную f(x) и ее максимум на [a,b] |
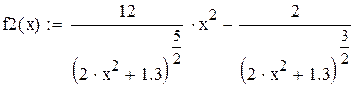
|
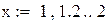
|

|
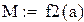
|
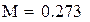
|
| Найдем значение n, при котором остаточный член будет меньше заданной точности |
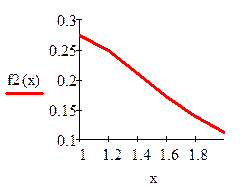
|
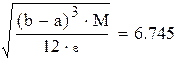
|
| Положим |
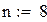
|
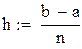
|
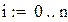
|
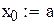
|
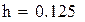
|
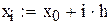
|
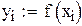
|
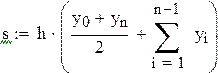
|
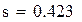
|
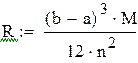
|
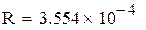
|
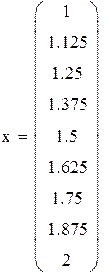
|
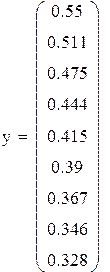
|
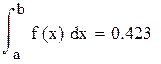
|
Рис. 8.2. Решение примера 8.1 в Mathcad

8.3 Формула Симпсона и ее остаточный член
Рис 8.2. Формула Симпсона
Найдем коэффициенты -Котеса для n=1
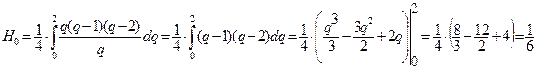 .
.
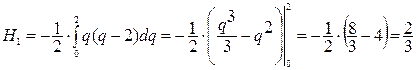
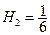
Подставим в формулу (8.3)
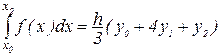 .
.
Если подынтегральная функция 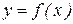 четырежды дифференцируема, то остаточный член квадратурной формулы Симпсонаравен:
четырежды дифференцируема, то остаточный член квадратурной формулы Симпсонаравен: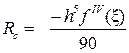
Дата добавления: 2017-05-18; просмотров: 778;
