Метод наименьших квадратов
Задача наименьших квадратов возникает в самых различных областях науки и техники, например, при статистической обработке данных.
Для линейной зависимости y=ax+b составляем функцию, которая представляет собой сумму квадратов отклонений от прямой: 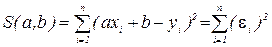 , где
, где 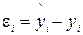 (
( 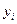 -табличное значение,
-табличное значение, 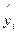 - эмпирическая формула). Надо определить такие значения параметров a и b , при которых функция двух переменных достигает минимума. Необходимым условием для этого является равенство нулю частных производных по a и b.
- эмпирическая формула). Надо определить такие значения параметров a и b , при которых функция двух переменных достигает минимума. Необходимым условием для этого является равенство нулю частных производных по a и b.
Возьмем частные производные по переменным a и b, приравняем их к нулю:
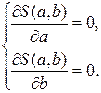
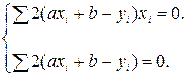
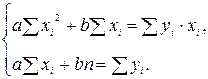
Получим систему линейных уравнений относительно неизвестных
a и b. Система называется нормальной для метода наименьших квадратов. Решаем систему по правилу Крамера:
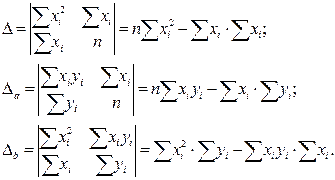
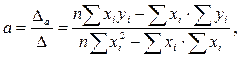
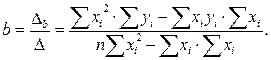
Если обозначить: 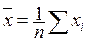 ,
, 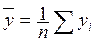 ,
,
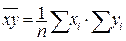 ,
, 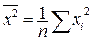 , то тогда можно записать
, то тогда можно записать
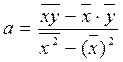 и
и 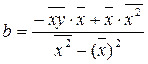 .
.
Метод выравнивания
К линейной функции можно привести любую функцию вида ψ(y)=aּφ(x)+b, для этого достаточно сделать замену переменных, z=ψ(y), t=φ(x). Тогда мы получим z=aּt+b.
Рассмотрим показательную функцию 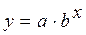 .
.
Прологарифмируем это равенство. Получим ln(y)=ln(a)+x ln(b). Сделаем замену переменных z= ln(y), t=x и обозначим А= ln(b) B= ln(a). После замены получим z=A t+b.
Аналогично делаются замены и для других функций из таблицы.
Таблица 7.1.
Таблица замен
| № | Вид функции | Замена переменных | Характерные точки | Отклонения |
| 1. | 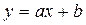
| 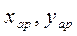
| 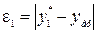
| |
| 2. | 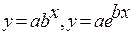
| 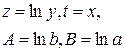
| 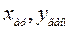
| 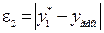
|
| 3. | 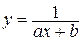
| 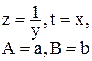
| 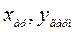
| 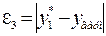
|
| 4. | 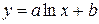
| 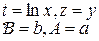
| 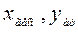
| 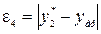
|
| 5. | 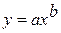
| 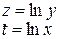 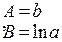
| 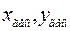
| 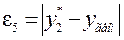
|
| 6. | 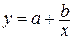
| 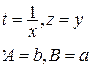
| 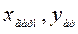
| 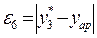
|
| 7. | 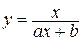
| 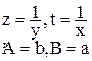
| 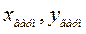
| 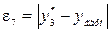
|
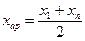 ,
, 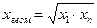 ,
, 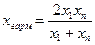 .
.
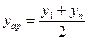 ,
, 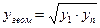 ,
, 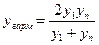 .
.
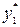 - табличное значение для xар;
- табличное значение для xар;
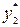 - табличное значение для хгеом;
- табличное значение для хгеом;
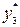 - табличное значение для хгарм.
- табличное значение для хгарм.
В таблице может не оказаться точек 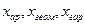 тогда точки
тогда точки 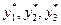 ,
, 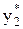 доопределяют по соседним точкам таблицы с помощью линейной интерполяции.
доопределяют по соседним точкам таблицы с помощью линейной интерполяции.
Для аналитических кривых существуют характерные точки, которые лежат на этих кривых. Например, если две точки принадлежат прямой, то и точка с координатами ( 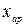 ,
, 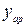 ) принадлежит той же прямой, если две точки принадлежат гиперболе, то и точка (xар,yгарм) также принадлежат этой гиперболе. В таблице через
) принадлежит той же прямой, если две точки принадлежат гиперболе, то и точка (xар,yгарм) также принадлежат этой гиперболе. В таблице через 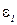 обозначено отклонение табличного значения
обозначено отклонение табличного значения 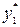 , соответствующего xар, от ординаты характерной точки
, соответствующего xар, от ординаты характерной точки 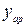 , через
, через 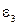 - отклонение табличного
- отклонение табличного 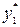 от ординаты характерной точки yгарм и т.д.
от ординаты характерной точки yгарм и т.д.
Остальные 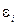 находятся аналогично, в зависимости от характерных точек. Функция, для которой
находятся аналогично, в зависимости от характерных точек. Функция, для которой 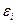 примет наименьшее значение и будет наиболее подходящей. После соответствующей замены переменных применяют метод наименьших квадратов.
примет наименьшее значение и будет наиболее подходящей. После соответствующей замены переменных применяют метод наименьших квадратов.
Пример 7.1
Бомба «Рейда» это техническое устройство для изучения легкоиспаряющихся жидкостей. В эксперименте на бомбе «Рейда» при постоянной температуре измеряется манометром избыточное давление паров нефти при различных соотношениях объёмов газовой и жидкой фаз. Определить эмпирическую зависимость давления паров нефти от соотношения объёмов газовой и жидкой фаз методом наименьших квадратов. Набор экспериментальных данных представлен в таблицах
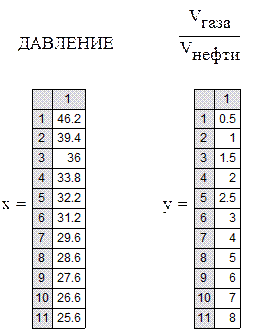
Для того, чтобы выбрать наиболее подходящую зависимость построим график по табличным данным
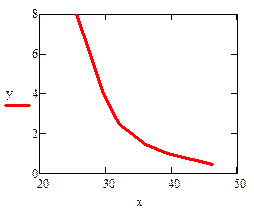
|
Можно предположить, что это будет :
1. показательная функция (строка 2 таблицы 7.1),
2. степенная функция (строка 5 таблицы 7.1),
3. дробно–рациональная функция (строка 3 таблицы 7.1).
Выберем ту функцию, для которой 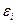 примет наименьшее значение.
примет наименьшее значение.
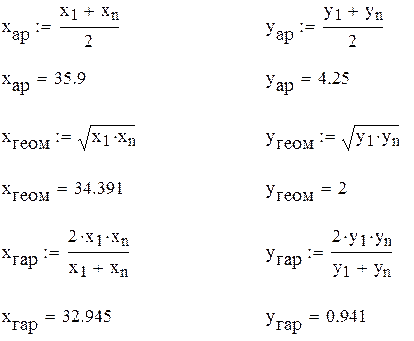
В таблице данных нет значений 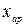 ,
, 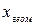 ,
, 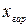 , подставляя
, подставляя 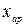 ,
, 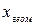 ,
, 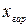 вместо v в формулу для линейной интерполяции, найдем соответствующие им значения функции
вместо v в формулу для линейной интерполяции, найдем соответствующие им значения функции 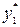 ,
, 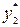 ,
, 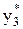 .
.
Формула для вычисления табличного значения для 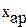 , , 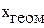 , , 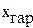 , с помощью линейной интерполяции , с помощью линейной интерполяции
|
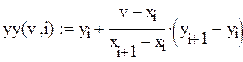
|
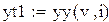
|
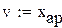
|
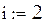
|
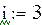
|
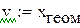
|
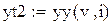
|
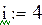
|
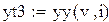
|
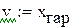
|
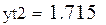
|
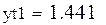
|
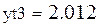
|
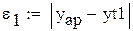
|
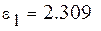
|
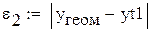
|
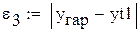
|
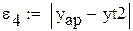
|
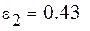
|
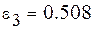
|
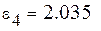
|
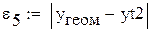
|
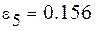
|
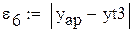
|
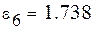
|
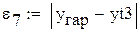
|
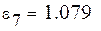
|
Самые маленькие 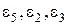 . Найдем методом выравнивания параметры для выбранных видов зависимостей. Будем искать аппроксимирующую функцию в виде
. Найдем методом выравнивания параметры для выбранных видов зависимостей. Будем искать аппроксимирующую функцию в виде
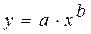 .
.
Делаем замену переменных
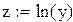
|
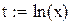
|

|

|
После замены точки ложатся близко к прямой. Параметры этой прямой A и B
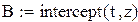
|
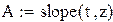
|
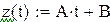
|
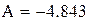
|
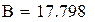
|
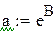
|
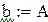
|
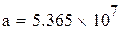
|
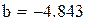
|
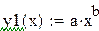
|
|
После замены z = At + B нашли A и B по методу наименьших квадратов, используя встроенные функции Mathcadа.
Функция slope(x,y) возвращает значение углового коэффициента.
Функция intercept(x,y) возвращает значение свободного параметра.
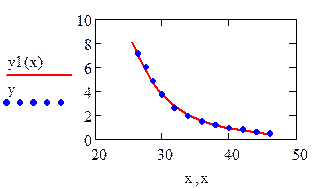
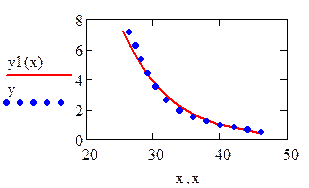
Возвращаемся к исходной функции 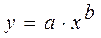 , строим её график и находим сумму квадратов отклонений от исходной таблицы значений. Можно также найти и среднеквадратичное отклонение.
, строим её график и находим сумму квадратов отклонений от исходной таблицы значений. Можно также найти и среднеквадратичное отклонение.
.

Из двух разных приближений одной и той же табличной функции лучшим считается то, для которого сумма квадратов отклонений меньше.
Для этой же таблицы данных рассмотрим приближение, заданное показательной функцией
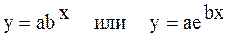 .
.
| Замена переменных |
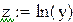
|
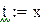
|
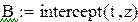
|
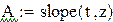
|
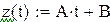
|
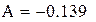
|
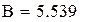
|
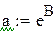
|
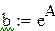
|
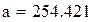
|
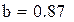
|
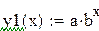
|
|
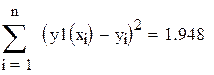
|
| среднеквадратичное отклонение. |
| сумма квадратов отклонений |
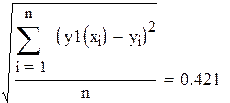
|
Для этой же таблицы данных рассмотрим приближение, заданное дробно-линейной функцией 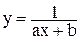 .
.
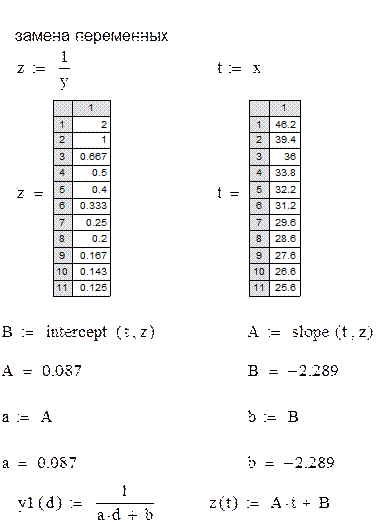
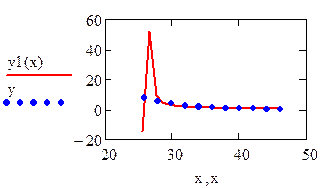
|

Рис. 7.2. Решение примера 7.1 в Mathcad
Лучшим приближением для этих экспериментальных данных будет степенная функция. 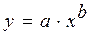
Дата добавления: 2017-05-18; просмотров: 1134;
