Классическое определение вероятности. Основные формулы исчисления вероятностей

Разберём весьма частный, однако, часто встречающийся случай: W состоит из конечного числа N равновероятных событий.

Понятие ''равновероятности'' здесь является исходным, неопределяемым. Основанием для суждения о равновозможности, равновероятности обычно слу­жит физическая симметрия, равноправие исходов. Понятие "вероятность" здесь уже является производным, определяемым: вероятностью P(A) события A называется

P(A)= ,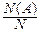

где N(A) – число элементарных событий, благоприятствующих событию A.

В этих условиях выведем основные формулы исчисления вероятностей.

1°. Вероятность достоверного события равна 1: P(W)=1. Это очевидно, так как  N(W)=N.

2°. Вероятность невозможного события равна 0: P(Æ)=0.  Это ясно, поскольку N(Æ)=0.

3°. P( 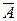)=1-P(A). Справедливость равенства следует из равенства N(A)+
+N( 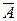)=N.

4°. 0£P(A)£1 для "A, поскольку 0£N(A)£N.

5°. AÍB Û P(A)£P(B), поскольку в этом случае N(A)£N(B).

6°. Для любых событий A и B: P(AB)£P(A), так как N(AB)£N(A).

7°. Теорема сложения для несовместимых событий. Если события A и B несовместимы, то вероятность их суммы равна сумме вероятностей:

P(A+B)=P(A)+P(B).

Действительно, N(A+B)=N(A)+N(B) и остаётся разделить это равенство на N.

8°. Теорема сложения в общем случае:

P(A+B)=P(A)+P(B)-P(AB).

Действительно, из определения суммы событий: N(A+B)=N(A)+N(B)-
-N(AB). Деля почленно это равенство на N, убеждаемся в справедливости теоремы.

9°. Обобщение теоремы сложения на n событий:

P(A₁+A₂+¼+A_n)= 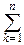(-1)^k+1 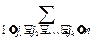P(A_j1A_j2¼A_jk).

Формула доказывается методом математической индукции несложно, но громоздко. Во внутренней сумме число слагаемых, очевидно, равно 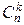и суммирование ведётся по всевозможным наборам различных натуральных индексов  j₁, j₂, ¼ , j_k.

10°. Условная вероятность.

Добавим к комплексу условий, реализация которых интерпретируется как опыт, ещё одно условие: произошло событие B; это возможно практически лишь в случае, когда P(B)>0. Все опыты, в которых B не произошло, мы как бы игнорируем. Считаем, что добавление события B к комплексу условий не нарушает равновероятности исходов и не меняет природы самих исходов. Теперь опыт может иметь лишь один из N(B) исходов, а из них событию A благоприятствуют N(AB) исходов. В соответствии с классическим определением, вероятность события A при условии, что произошло событие B, равна:

P(A|B)== = .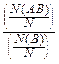

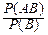Таким образом, по существу, условная вероятность ничем не отличается от обычной, безусловной вероятности.

В случае, если AÍB, формула для условной вероятности упрощается:

P(A|B)= ,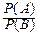

так как здесь AB=A.

11°. Теорема умножения: вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло:

P(AB)=P(B)×P(A|B)=P(A)×P(B|A).

Первая из этих формул для P(B)>0 является лишь формой записи формулы пункта 10° для условной вероятности; вторая получена из неё перестановкой местами A и B, что для P(A)>0 возможно. Вместе с тем ясно, что теорема умножения верна и для случая P(A)=0 или P(B)=0, но при этом она становится тривиальной и бессодержательной.

12°. Независимость событий.

Будем говорить, что событие A не зависит от события B, если P(A|B)=P(A). В этом случае теорема умножения упрощается: P(AB)=P(A)×P(B).

И наоборот, для событий, имеющих положительную вероятность, из последней формулы следует независимость события A от B:

P(A|B)= 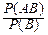= =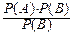P(A).

Таким образом, второе эквивалентное определение независимости: события A и B, имеющие положительные вероятности, независимы, если вероятность их произведения равна произведению их вероятностей: P(AB)=P(A)P(B). События A и B в этом определении симметричны: если событие A не зависит от B, то и B не зависит от A.

Если события A и B независимы, то независимы также и события A и .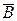

Действительно:

P( 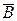|A)+P(B|A)= 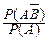+ 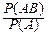= = 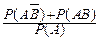=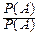1,

откуда:

P( 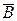|A)=1-P(B|A)=1-P(B),

а это и доказывает наше утверждение.

Ясно, что независимы также и события , .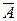

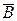Если события A и B независимы, то они не могут быть несовместимыми: если A и B – одновременно несовместимы и независимы, то, с одной стороны, AB=Æ и P(AB)=0, а, с другой, – P(AB)=P(A)×P(B), что противоречит предположению о положительности вероятностей P(A) и P(B).

Обобщение понятия независимости на n событий: события A₁, A₂, ¼ , A_nназываются независимыми в совокупности, если для любого набора различных индексов j₁, j₂, ¼ , j_k вероятность произведения событий A_j1A_j2¼A_jk равна произведению вероятностей событий A_j1, A_j2, ¼ , A_jk:

P(A_j1A_j2¼A_jk)=P(A_j1)×P(A_j2)×¼×P(A_jk).

Можно думать, что для независимости событий в совокупности достаточно попарной независимости, Конкретные примеры, однако, доказывают, что это не так.

Таким образом, для независимых событий легко вычислять вероятность произведения, а для несовместимых событий легко вычислять вероятность суммы.

Если события A₁, A₂, ¼ , A_n независимы, то

P(A₁+A₂+¼+A_n)=P( 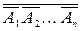)=1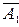-P( )×P( 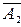)×¼×P( ).

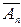Если события A₁, A₂, ¼ , A_n несовместимы, то

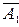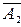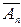P( × ×¼× )=P( 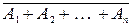)=1-P(A₁+A₂+¼+A_n)=1- 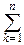P(A_k).

13°. Теорема умножения для n событий:

P(A₁A₂¼A_n)=P(A₁)×P(A₂¼A_n|A₁).

Учитывая, что условные вероятности ничем не отличаются от безусловных – лишь добавляется к комплексу условий ещё одно, которое в дальнейшем терять или отбрасывать нельзя, – можем продолжить:

P(A₁A₂¼A_n)=P(A₁)×P(A₂|A₁)×P(A₃¼A_n|A₁A₂) ¼ .

Окончательно:

P(A₁A₂¼A_n)=P(A₁)×P(A₂|A₁)×P(A₃|A₁A₂)×¼×P(A_n|A₁A₂¼A_n-1).

Эта теорема позволяет дать ещё одно определение независимости в совокупности: события A₁, A₂, ¼ , A_n, имеющие положительные вероятности, независимы в совокупности, если для любого набора неравных индексов

P(A_j1A_j2¼A_jk|A_i1A_i2¼A_im)=P(A_j1A_j2¼A_jk),

что легко устанавливается по теореме умножения и формуле для условных вероятностей.

14°. Формула полной вероятности.

Пусть A₁, A₂, ¼ , A_n– любое разбиение пространства W, B – любое событие. Тогда B=BW=B(A₁+A₂+¼+A_n)=BA₁+BA₂+¼+BA_n и получаем формулу полной вероятности:

P(B)= 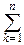P(BA_k)= 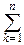P(A_k)×P(B|A_k).

Обычно A₁, A₂, ¼ , A_n – взаимоисключающие друг друга ситуации, в которых может происходить событие B.

15°. Формулы Байеса.

В обозначениях предыдущего пункта:

P(A_k|B)= 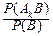= 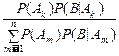, k=1, 2, ¼ , n,

и мы получили формулы Байеса, которые называют также формулами вероятностей гипотез: если событие B может произойти лишь с одним и только одним из событий A₁, A₂, ¼ , A_nи оно действительно произошло, то, спрашивается, с каким из событий A_kоно произошло? Можно сделать n гипотез и, соответственно, формулы Байеса дают апостериорные вероятности P(A_k|B) для этих гипотез, выражая их через априорные вероятности P(A_m) и условные вероятности P(B|A_m) того, что в условиях m-ой гипотезы произойдёт событие B.

Таковы основные формулы исчисления вероятностей. Они получены в условиях весьма частного случая – классической схемы, т. е. для пространства конечного числа N равновероятных элементарных событий. В этой схеме число событий, которым благоприятствуют ровно k исходов, равно 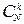, а общее число различных событий, следовательно, равно 2^N.

Весьма неожиданно, что все полученные формулы являются общими и в действительности сохраняют свою силу для любого пространства элементарных событий. Покажем это.