Распределение Стьюдента

Пусть даны две независимые случайные величины X~N(0, 1), и c_n.

Определим случайную величину T_n равенством: T_n= 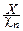 и найдём закон её распределения.

Совместная плотность вероятности двумерной случайной величины (X, c_n) равна:

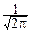
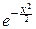
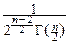
p(x, y)= 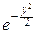y^n-1, для -¥<x<+¥, 0<y<+¥.

Функция распределения дроби T_n равна:

F_Tⁿ(t)=P{T_n<t}=P{ 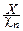<t}=P{X<tc_n}.

Неравенству X<tc_n благоприятствуют точки, занимающие область, заштрихованную на Рис. 3:

y Рис. 3. x

Этой области досталась вероятность:

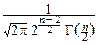
F_Tⁿ(t)=P{T_n<t}= dy p(x, y)dx= dy 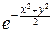y^n-1dx.

Отсюда находим плотность вероятности:

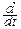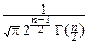
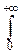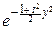p_Tⁿ(t)= F_Tⁿ(t)= y^n-1 ydy.

Отметим, что в интеграле t играет роль параметра и сделаем замену переменной:

u= 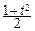y² Þ 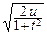y=  Þ dy= .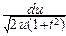

Имеем:

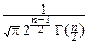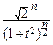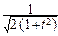
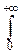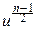p_Tⁿ(t)= × × e^-u du

и, выражая интеграл через гамма-функцию, мы можем записать плотность распределения Стьюдента в следующем – окончательном виде:

p_Tⁿ(t)= × .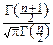

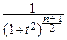Отметим, что при n=1 из этой формулы получается плотность распределения Коши:

p_T¹(t)= ,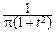

т. е. случайную величину, распределенную по закону Коши, можно считать отношением двух независимых случайных величин, X= 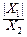, где X_i~N(0, 1), i=1, 2.

Замечание. Часто случайную величину T_nопределяют с дополнительным множителем: T_n= 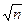× 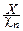. В этом случае плотность вероятности имеет вид:

p_Tⁿ(t)= 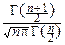×(1+ ) .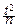

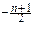Дополнительные множители появляются и в выражении для функции распределения.