Одномерные случайные величины

Пусть имеется вероятностное пространство (W, Å, P(×)) Определим на W числовую функцию X=X(w): каждому элементарному событию w приведено в соответствие вещественное число X(w).Такая функция называется случайной величиной. Мы ставим опыт, получаем элементарное событие w, смотрим, какое число X(w)=x было приведено ему в соответствие, и говорим: в опыте случайная величина X приняла значение x.

Рассмотрим простейший случай: число возможных значений случайной величины X конечно или счётно: x₁, ¼ , x_k, ¼ Такую случайную величину называют дискретной. Законом распределения дискретной случайной величины называют совокупность вероятностей её возможных значений: p_k=P{X=x_k}. Будем предполагать, что события {X=x_k} содержатся в поле событий Å, и тем самым вероятности p_kопределены.

Очевидно, одно и только одно из своих значений случайная величина обязательно примет. Поэтому выполняется равенство

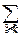p_k=1,

называемое иногда условием нормировки в дискретном случае.

Задать случайную величину значит задать закон её распределения: т. е. указать её возможные значения и распределение вероятностей между ними.

В общем случае общепринятый способ задания случайной величины даёт так называемая функция распределения:

F(x)=P{X<x}.

Она указывает, какая вероятность досталась не отдельным точкам, а полуоси левее точки x, не включая саму точку x. Приходится дополнительно предполагать, что событие {X<x}ÎÅ, в противном случае функция распределения была бы не определена.

Дискретную случайную величину можно задавать её функцией распределения. Нетрудно сообразить, что это будет ступенчатая функция с разрывами в точках x_kи скачками p_kв этих точках:

F(x)=P{X<x}= 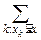P{X=x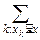_k}= p_k,

где суммирование ведётся по всем тем возможным значениям X, которые оказались меньше x.

Если существует такая функция p(x), которая позволяет представить функ­цию распределения интегралом:

F(x)= 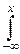p(x)dx,

то случайная величина X называется непрерывной, а p(x) – плотностью вероятности случайной величины X.

Функция распределения F(x) непрерывной случайной величины является непрерывной функцией (отсюда и название случайной величины), и, более того, – дифференцируемой функцией: F^¢(x)=p(x).

В более общем случае случайная величина X может принадлежать к смешанному типу: вероятность распределяется как между отдельными точками (дискретная составляющая), так и на интервалах (непрерывная составляющая). Если отдельным точкам x_kдостались вероятности p_k, а остальная вероятность пошла на непрерывное распределение с линейной плотностью p(x), то:

F(x)=P{X<x}= 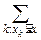P{X=x_k}+ 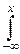p(x)dx.

Если суммарная вероятность, доставшаяся точкам x_kслучайной величины X смешанного типа, равна A ( 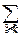p_k=A), а на непрерывное распределение X ухо­дит вероятность B, ( 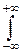p(x)dx=B), то A+B=1.

Можно считать, что случайная величина X является смесью двух случайных величин: дискретной Y с возможными значениями x_kи вероятностями 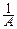p_kи непрерывной Z с плотностью 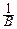p(x). Функция распределения X имеет вид: F(x)=AF_Y(x)+BF_Z(x).

Вообще, если имеются случайные величины X_i, i=1, 2, ¼ , n с функциямираспределения F_Xi(x), то смесью этих случайных величин называют случайную величину с функцией распределения

F(x)= 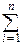A_iF_Xi(x),

где числа A_iудовлетворяют условиям: 0£A_i£1, A₁+A₂+¼+A_n=1, и играют роль весовых множителей, они регулируют вклад в смесь отдельных составляющих. Функция F(x), очевидно, обладает необходимыми свойствами функции распределения и может задавать случайную величину.

Основные свойства функции распределения F(x)
и плотности вероятности p(x)

1°. Считаем, что случайная величина X или совсем не принимает значений ±¥ или почти наверное их не принимает: P{X=+¥}=P{X=-¥}=0. При этом предположении:

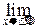F(x)=F(-¥)=0, 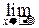F(x)=F(+¥)=1.

2°. F(x) – монотонно-неубывающая функция:

x₁<x₂ Þ F(x₁)£F(x₂).

Действительно: {X<x₂}={X<x₁}+{x₁£X<x₂}. Справа стоит сумма двух несовместимых событий. Поэтому:

P{X<x₂}=P{X<x₁}+P{x₁£X<x₂},

или:

F(x₂)=F(x₁)+P{x₁£X<x₂}

и неравенство F(x₂)³F(x₁) следует из неотрицательности вероятности P{x₁£X<
<x₂}.

3°. В доказательстве второго свойства мы выразили через функцию распределения вероятность попадания случайной величины X в полуоткрытый интервал:

P{x₁£X<x₂}=F(x₂)-F(x₁).

4°. Перепишем последнее равенство, взяв x₁=x, x₂=x+e, e>0:

P{x£X<x+e}=F(x+e)-F(x).

Перейдём здесь к пределу при e®0: P{X=x}= 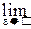F(x+e)-F(x)=F(x+0)-F(x). Таким образом, для любой случайной величины X вероятность любого конкретного значения равна скачку F(x+0)-F(x) её функции распределения в точке x. Во всех точках непрерывности F(x) этот скачок и, следовательно, вероятность P{X=x}, равны нулю. Для непрерывных случайных величин все точки таковы, и ни одной из них не досталось положительной вероятности.

Если мы наблюдаем непрерывную случайную величину и получили значение X=x, то мы получили пример события A={X=x}, вероятность которого равна нулю, которое, однако, произошло, а событие 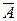 ={X¹x}, вероятность которого рана единице, не произошло. Ясно, что повторить появление события A почти наверное не удастся.

Так как функция распределения определена равенством F(x)=P{X<x}, где под знаком вероятности стоит строгое неравенство, то вероятность, возможно сосредоточенная в точке x, не учитывается, поэтому F(x) – функция, непрерывная слева:

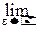F(x-e)=F(x-0)=F(x).

5°. Теперь нетрудно выразить через F(x) вероятность попадания случайной величины в произвольный интервал:

P{x₁£X£x₂}=F(x₂+0)-F(x₁),
P{x₁<X<x₂}=F(x₂)-F(x₁+0),
P{x₁<X£x₂}=F(x₂+0)-F(x₁+0).

6°. Плотность вероятности p(x) неотрицательна. Это следует из монотонного неубывания F(x).

7°. Переходя к пределу при x®+¥ в равенстве F(x)= 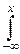p(x)dx, и учитывая, что F(+¥)=1, получим условие нормировки для непрерывной случайной величины:

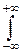p(x)dx=1.

Геометрический смысл этого равенства: площадь под кривой плотности вероятности всегда равна единице.

8°. Общее правило вычисления вероятностей для дискретной и непрерывной случайной величины: если A –– некоторое числовое множество на вещественной оси, то

P{XÎA}= 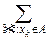P{X=x_k},
P{XÎA}= 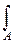p(x)dx

и ясно, что в непрерывном случае вероятность событий {XÎA} определена лишь для таких множеств A , для которых имеет смысл интеграл 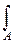p(x)dx.

9°. Мы считаем, что задавая произвольную функцию F(x) с обязательными свойствами функции распределения: монотонное неубывание, непрерывность слева, F(-¥)=0, F(+¥)=1, – мы задаём некоторую случайную величину. Если F(x) – ступенчатая функция, то она задаёт дискретную случайную величину: точки скачков – её возможные значения, величины скачков – их вероятности.

Дискретную случайную величину можно задать таблицей её возможных значений и их вероятностей: x_k, p_k, k=1, 2, ¼ , n, лишь бы были "p_k³0 и 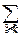p_k=1.

Непрерывную случайную величину можно задать плотностью вероятности p(x). В качестве таковой может служить любая неотрицательная функция, удовлетворяющая условию нормировки: 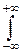p(x)dx=1.