Понятие об аксиоматическом построении теории вероятностей
Пусть дано пространство элементарных событий W. Множество Å событий A, B, C, ¼ назовём полем событий, если
а) WÎÅ;
б) A, BÎÅ Þ A+BÎÅ, ABÎÅ, 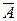 ÎÅ,
ÎÅ, 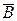 ÎÅ.
ÎÅ.
Таким образом, введённые действия с событиями: сложение, умножение и переход к противоположному событию – не выводят нас из поля событий, поле событий замкнуто относительно этих операций.
Очевидно, также, что ÆÎÅ.
Примем следующие три аксиомы:
I. Любому событию A из поля событий Å приведено в соответствие неотрицательноечисло P(A), называемое вероятностью события A.
II. P(W)=1: вероятность достоверного события равна единице.
III. Аксиома сложения. Вероятность суммы несовместимых событий равна сумме их вероятностей.
Если A1, A2, ¼ , An– попарно несовместимые события, то
P(A1+A2+¼+An)= 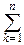 P(Ak).
P(Ak).
Тройка (W, Å, P(×)) называется вероятностным пространством.
Таким образом, поле событий Å является областью определения вероятностной функции P(×), при этом, как будет показано ниже (4°), отрезок [0; 1] является областью её значений.
Все пятнадцать формул исчисления вероятностей оказываются следствием трёх только что введённых аксиом. Действительно:
1°. P(W)=1 по II аксиоме.
2°. W+Æ=W, WÆ=Æ, поэтому по III аксиоме: P(W)+P(Æ)=P(W), откуда P(Æ)=0.
В классической схеме были справедливы и обратные утверждения: если P(A)=1, то событие A – достоверное; если P(A)=0, то событие A – невозможное. В общей же схеме обратные утверждения, вообще говоря, ошибочны. Приходится вводить особые названия для событий единичной и нулевой вероятности: если P(A)=1, то говорят, что событие A происходит почти наверное, если P(A)=0, говорят, что событие A почти наверное не происходит. Пожалуй, именно это различие значительно усложняет строгую теорию вероятностей по сравнению с классическим случаем.
3°. A+ 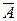 =W и A
=W и A 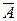 =Æ. Поэтому по аксиомам III и II: P(A)+P(
=Æ. Поэтому по аксиомам III и II: P(A)+P( 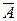 )=P(W)=1. Отсюда: P(
)=P(W)=1. Отсюда: P( 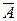 )=1-P(A).
)=1-P(A).
4°. По аксиоме I: P(A)³0. Так как P(A)+P( 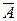 )=P(W)=1, и, ввиду аксиомы I: P(
)=P(W)=1, и, ввиду аксиомы I: P( 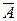 )³0, то P(A)£1. Итак, для любого события A: 0£P(A)£1.
)³0, то P(A)£1. Итак, для любого события A: 0£P(A)£1.
5°. Если AÌB, то B=A+ 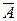 B, и слагаемые здесь несовместимы. По аксиоме III: P(B)=P(A)+P(
B, и слагаемые здесь несовместимы. По аксиоме III: P(B)=P(A)+P( 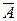 B); по I аксиоме: P(
B); по I аксиоме: P( 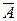 B)³0; поэтому P(B)³P(A).
B)³0; поэтому P(B)³P(A).
6°. Для любых двух событий A и B: P(AB)£P(A).
Действительно: A=AB+A 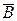 и по аксиомам III и I:
и по аксиомам III и I:
P(A)=P(AB)+P(A 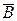 )³P(AB).
)³P(AB).
7°. Формула P(A+B)=P(A)+P(B) в случае, когда AB=Æ, верна по аксиоме III.
8°. Докажем теорему сложения для двух событий:
P(A+B)=P(A)+P(B)-P(AB).
Очевидно,
|
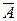 ,
,B=AB+B
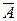 ,
,
причём в обоих равенствах справа слагаемые несовместимы. По III аксиоме:
|
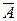 ),
),P(B)=P(AB)+P(B
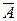 ).
).
Вычитая почленно нижнее равенство из верхнего, получим теорему сложения.
9°. Теорема сложения для n событий
P(A1+A2+¼+An)= 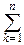 (-1)k+1
(-1)k+1 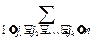 P(Aj1Aj2¼Ajk)
P(Aj1Aj2¼Ajk)
является прямым следствием теоремы сложения для двух событий.
10°. Формула для условной вероятности
P(A|B)= 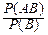
является определением условной вероятности в предположении, что вероятность P(B) ненулевая: P(B)>0. Вероятность P(A|B) показывает, какая часть вероятности P(B) приходится на долю события A.
11°. Прямым следствием определения условной вероятности оказывается формула:
P(AB)=P(B)×P(A|B)=P(A)×P(B|A).
12°. Совершенно так же, как и в классической схеме, на основе последних формул строится понятие независимости событий: события A и B независимы в том и только в том случае, когда P(AB)=P(A)×P(B).
13°. Теорема умножения для n событий
P(A1A2¼An)=P(A1)×P(A2|A1)×P(A3|A1A2)×¼×P(An|A1A2¼An-1)
является прямым следствием теоремы умножения для двух событий.
14°, 15°. Выводы формулы полной вероятности и формул вероятностей гипотез воспроизводятся без изменений: для любого события B и любого разбиения пространства W (W=A1+A2+¼+An):
P(B)= 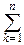 P(Ak)×P(B|Ak),
P(Ak)×P(B|Ak),
P(Ak|B)= 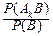 =
= 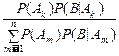 , k=1, 2, ¼ , n.
, k=1, 2, ¼ , n.
В более полных, чем наш, курсах теории вероятностей приходится рассматривать также и суммы бесконечного числа событий и, соответственно, требовать, чтобы эта операция не выводила из поля событий: для бесконечной последовательности попарно несовместимых событий A1, A2, ¼ , An, ¼ требуют, чтобы 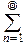 AnÎÅ. Такие поля событий называются борелевскими полями или сигма-алгебрами. Приходится для борелевского поля событий усиливать аксиому III, распространяя её и на бесконечные суммы попарно несовместимых событий:
AnÎÅ. Такие поля событий называются борелевскими полями или сигма-алгебрами. Приходится для борелевского поля событий усиливать аксиому III, распространяя её и на бесконечные суммы попарно несовместимых событий:
P( 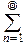 An)=
An)= 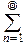 P(An).
P(An).
Любопытно отметить, что в изложенном аксиоматическом построении теории вероятностей не нашлось места такому понятию, как событие "произошло" или "не произошло". Теория вероятностей оказывается частью теории меры, причём характерными свойствами вероятностной меры оказываются её неотрицательность: P(A)³0 и нормированность на единицу: P(W)=1. Просматривая выведенные свойства вероятностной функции P(×), можно заметить, что она ведёт себя подобно массе: единичная "масса вероятности" распределяется в пространстве W. Если нас интересует вероятность некоторого события A, то мы должны подсчитать, сколько этой массы досталось множеству A.
Дата добавления: 2017-09-19; просмотров: 468;