Вычисление дискретного преобразования Фурье
Итак, будем искать способы вычисления выражений 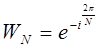 ;
; 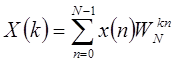 . Обратное преобразование Фурье для дискретного сигнала для дискретного сигнала:
. Обратное преобразование Фурье для дискретного сигнала для дискретного сигнала: 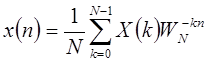 . В этих выражениях как
. В этих выражениях как 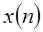 так и
так и 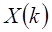 могут быть комплексными. Выражения для прямого и обратного преобразований отличаются только знаком экспоненты и скалярным коэффициентом
могут быть комплексными. Выражения для прямого и обратного преобразований отличаются только знаком экспоненты и скалярным коэффициентом 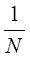 . Поэтому рассуждения касающиеся вычислительных процедур применимы к обоим выражениям.
. Поэтому рассуждения касающиеся вычислительных процедур применимы к обоим выражениям.
Так как 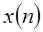 может быть комплексным, то можно записать
может быть комплексным, то можно записать
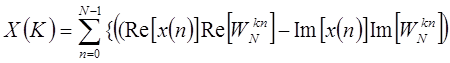
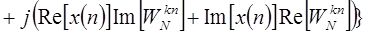 , ,
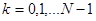
| (1.53) |
Отсюда видно, что для каждого значения k при непосредственном вычислении 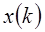 требуется 4N умножений и (4N-2) сложений действительных чисел. Так как
требуется 4N умножений и (4N-2) сложений действительных чисел. Так как 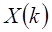 должно вычисляться для N различных значений K, непосредственное вычисление дискретного преобразования Фурье последовательности
должно вычисляться для N различных значений K, непосредственное вычисление дискретного преобразования Фурье последовательности 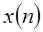 требует 4
требует 4 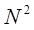 умножений и
умножений и 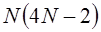 сложений действительных чисел.
сложений действительных чисел.
Так как количество вычислений, а следовательно, и время вычислений приблизительно пропорционально 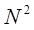 , то ясно, что при прямом методе необходимое число арифметических операций становится очень большим.
, то ясно, что при прямом методе необходимое число арифметических операций становится очень большим.
Большинство подходов к улучшению эффективности вычисления ДПФ использует следующие свойства величин 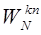 .
.
1. 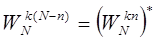 (комплексно сопряжены)
(комплексно сопряжены)
2. 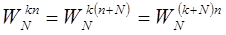 , где
, где 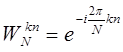
Дата добавления: 2017-08-01; просмотров: 627;
