Свойства z-преобразования
Линейность: если 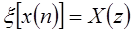 и
и 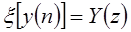 , то
, то 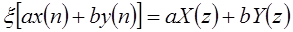 , где область сходимости равна, по крайней мере, пересечению областей сходимости
, где область сходимости равна, по крайней мере, пересечению областей сходимости 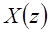 и
и 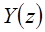 .
.
Сдвиг: если 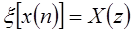 , то
, то 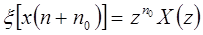 .
.
Умножение на экспоненциальную последовательность: 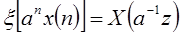 .
.
Дифференцирование: 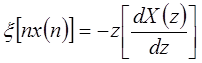 .
.
Свертка последовательностей: если 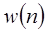 - свертка двух последовательностей
- свертка двух последовательностей 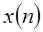 и
и 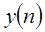 , то z-преобразование
, то z-преобразование 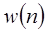 равно произведению z-преобразований
равно произведению z-преобразований 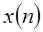 и
и 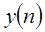 , т.е. если
, т.е. если 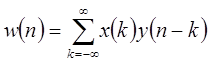 , то
, то 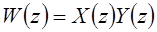 .
.
Теорема о комплексной свертке. В непрерывном случае свертка временных функций приводит к произведению преобразований Фурье и, аналогично, свертка преобразований Фурье получается из произведения временных функций.
В случае последовательностей и z-преобразований нельзя ожидать такого соотношения из-за того, что последовательности дискретны, а их z-преобразования непрерывны. Однако можно вывести похожее соотношение: если 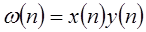 , то
, то 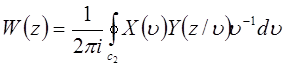 .
.
Соотношение Парсеваля. Известно соотношение Парсеваля для преобразования Фурье. Обобщение этого соотношения на z-преобразование следует из теоремы о комплексной свертке. В частности, мы рассмотрим две комплексные последовательности 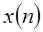 и
и 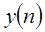 . Тогда соотношение Парсеваля утверждает, что
. Тогда соотношение Парсеваля утверждает, что
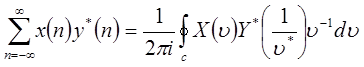 . .
| (1.43) |
Контур интегрирования выбирается в пересечении областей сходимости 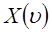 и
и 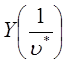 .
.
Передаточная функция. В частотной области соотношение входным и выходным сигналами получается простым умножением преобразования Фурье входного сигнала на преобразование Фурье импульсной характеристики.
Более общим образом можно описать линейные стационарные системы с помощью z-преобразования импульсной характеристики.
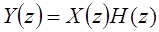 . .
| (1.44) |
Часто z-преобразование импульсной характеристики называется передаточной или системной функцией. Передаточная функция на единичной окружности (т.е. при 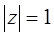 ) является частотной характеристикой системы.
) является частотной характеристикой системы.
Если область сходимости передаточной функции включает единичную окружность, то система устойчива и наоборот.
Если систему можно описать линейным разностным уравнением с постоянными коэффициентами, то ее передаточная функция является отношением полиномов.
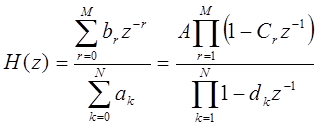
| (1.45) |
Следовательно, с точностью до скалярного множителя А передаточная функция может быть полностью описана картиной полюсов и нулей в z-плоскости.
Соотношение (1.45) не содержит указаний об области сходимости передаточной функции. Это находится в соответствии с тем фактом, что разностное уравнение неоднозначно определяет импульсную характеристику линейной стационарной системы. Для данного отношения полиномов различные способы выбора области сходимости приведут к различным импульсным характеристикам, но они все будут удовлетворять одному и тому же разностному уравнению. Если предположить, что система устойчива, то нужно выбрать кольцевую область, включающую единичную окружность.
z-преобразования некоторых функций
| Функция времени | Преобразование Лапласа | z-преобразование |
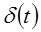 (штырек) (штырек)
| ||
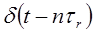
| 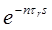
| 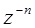
|
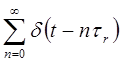
| 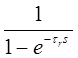
| 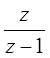
|
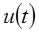 (ступенька) (ступенька)
| 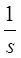
| 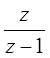
|
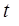
| 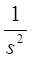
| 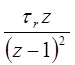
|
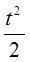
| 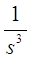
| 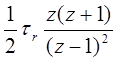
|
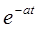
| 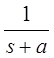
| 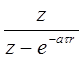
|
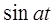
| 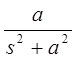
| 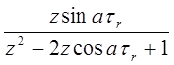
|
Дата добавления: 2017-08-01; просмотров: 997;
