Алгоритм БПФ с прореживанием по времени
Чтобы достичь существенного улучшения эффективности необходимо разложить вычисления ДПФ на набор ДПФ меньшего порядка. Алгоритмы, в которых это разложение основано на разложении последовательности 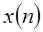 на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени.
на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени.
Рассмотрим частный случай 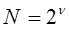 .
. 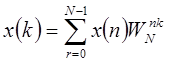 ,
, 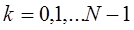 . Разделим
. Разделим 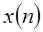 на четные и нечетные точки:
на четные и нечетные точки: 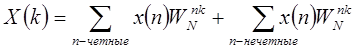 , или, заменяя индексы суммирования на
, или, заменяя индексы суммирования на 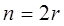 при четном n и
при четном n и 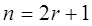 при нечетном, получим
при нечетном, получим 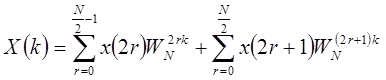 =
= 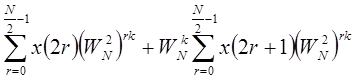 , т.к.
, т.к. 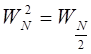 , то
, то
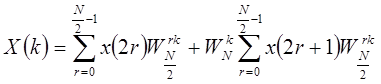 = = 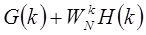
| (1.54) |
Каждая из сумм является N/2 точечным ДПФ. Первая сумма N/2 точечное ДПФ четных точек исходных последовательностей, а вторая – N/2 точечное ДПФ нечетных точек исходных последовательностей. Хотя индекс k простирается на N значений, k=0,1,…,N-1, каждая из сумм требует вычислений только для k от 0 до N/2-1, т.к. G(k) и H(k) периодичны по k с периодом N/2.
После того, как ДПФ, соответствующие двум суммам в (1.54), вычислены, они объединяются и дают N-точечное ДПФ 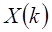 .
.
 |
Рис. 1.4. Разложение 8-точечного ДПФ
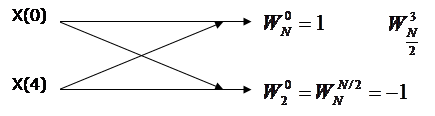 |
Рис. 1.5.
 |
Разложение 4-точечного ДПФ.
Рис. 1.6. 2-х точечное ДПФ.
Проведя разложение максимально возможное число раз, получим общее число комплексных умножений и сложений, равное 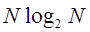 .
.
Дата добавления: 2017-08-01; просмотров: 977;
