Построение линий влияния

Методику построения рассмотрим на примере фермы (рис.3.47 а). Единичная сила Р = 1 перемещается по нижнему поясу. Линии влияния опорных реакций ферм (рис. 2.47 б), не отличаются от линий влияния опорных реакций балок по способу построения и форме.

Линии влияния усилий в стержнях фермы

Линии влияния усилия О_3-4.Проводим разрез I - I, пересекающий три стержня, в том числе искомый. Подвижную единичную силу располагаем на правой части фермы. Отбросим ее. Действие отброшенной правой части заменяем усилиями в разрезанных стержнях, полагая, что они растягивающие, т. е. направлены от узлов. Рассматриваем равновесие левой части фермы. К ней приложено четыре усилия: R_A, O_3-4, D_3-13 и U_13-14. Необходимо составить такое уравнение статики, в которое в качестве единственного неизвестного входило бы интересующее нас усилие O_3-4. Очевидно, это уравнение ∑М₁₃ = 0.

Моментную точку выбираем на пересечении стержней 13-3 и 13-14. Получаем:

+ R_A ·2d + O_3-4 ·r₁ = 0.

Отсюда O_3-4 = - 2d · R_A /r₁. (3.38)

Из уравнения (3.38) следует, что линия влияния усилия отличается от линии влияния опорной реакции R_A только тем, что ее ординаты умножены на постоянную величину (-2d / r₁ ).

Для построения линии влияния R_A на левой опоре следова­ло бы отложить ординату, равную + 1 (рис. 3.47 б). При построении линии влияния O_3-4 налевой опоре откладываем ординату, равную (-2d / r₁ ) в том же масштабе (рис. 3.47 г). На правой опоре орди­ната остается равной нулю. Соединяем эти две точки прямой. Из полученного графика в качестве линии влияния O_3-4 мы можем взять только часть - от опоры В до моментной точки 13, так как уравнение (3.38) составлено при условии, что единичный груз Р = 1 находится справа от разреза, а именно в пределах от опоры В до точки 13. Это не вся линия влияния, а только ее пра­вая ветвь. Для того, чтобы построить левую ветвь линии влия­ния O_3-4, необходимо рассмотреть равновесие правой части фермы (относительно разреза I - I), предварительно переместив единичный груз Р = 1 на левую часть фермы и отбросив ее. Составляем уравнение статики

∑М₁₃ = 0; -R_B ·4d - O_3-4 ·r₁ = 0.

Отсюда O_3-4 = - 4d ·R_B /r₁. (3.39)

Для построения графика уравнения (3.39) на правой опоре откладываем ординату, равную (- 4d /r₁) в том же масштабе, на левой - ординату, равную нулю. Соединяем эти две точки прямой. Из полученного графика берем только левую часть - от опоры А до точки 13, которая и будет левой ветвью линии влияния O_3-4 (рис. 3.47 г).

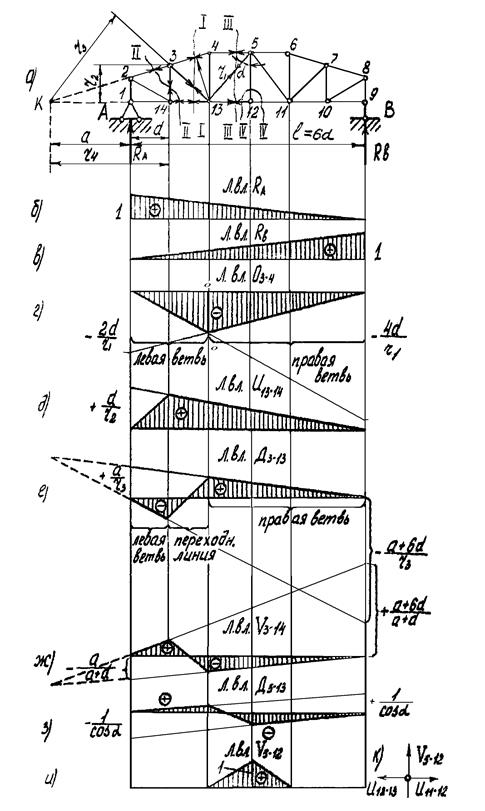
Рис. 3.47. Схема построения линий влияния усилий в стержнях фермы

Графики уравнений (3.38) и (3.39) на рис.3.47 г пересекаются под моментной точкой 13. Это не случайно, а за­кономерно, что можно доказать, рассмотрев подобие двух пресекающихся по линии О-О треугольников.

Для треугольника слева от линии О-О с катетом 2d/r₁ отношение его катетов можно записать: 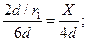откуда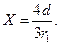

Для треугольника справа от линии О-О с катетом 4d/r₁ отношение его катетов можно записать: 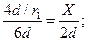откуда 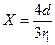. Получили, что линия О-О имеет одинаковую длину для обоих пересекающихся по этой линии треугольников. С учетом этого обстоятельства в подобных случаях ли­нии влияния усилий можно строить упрощенным способом. Достаточно построить один из двух графиков и снести на него моментную точку. Это будет вершина линии влияния, остальное построе­ние, очевидно, не требует пояснений.

Линия влияния усилия U_13-14. Порядок построения аналогичен принятому при построении линии влияния O_3-4 . Используем тот же разрез I - I. Моментной точкой теперь будет точка 3. Рассматривая равновесие левой части фермы, составляем уравнение ∑М₃ = 0:

- U_13-14 · r₂ + R_A ·d = 0.

Отсюда получаем: U_13-14 = d · R_A / r₂. (3.40)

Строим график уравнения (3.40). На левой опоре откладываем ординату, равную (d / r₂ ), в том же масштабе (рис. 3.47 д). На правой опоре ордината равна нулю. Соединяем эти две точки прямой, сносим на нее моментную точку и соединяем с левой опорой. Ординаты линии влияния положительны, т.е. стержень U_13-14 растянут при всех возможных положениях единичного груза в пределах пролета L .

Линия влияния _усилия D_3-13. Используем тот же разрез I - I. Моментной точкой будет точка «К» - за пределами фермы на пересечении стержней 3-4 и 13-14. Рассматривая равновесие левой части фермы, состав­ляем уравнение ∑М_К = 0: D_3-13 ·r₃ - R_A ·a = 0.

Отсюда получаем D_3-13 = + a· R_A / r₃. (3.41)

Строим график уравнения (3.41). На левой опоре откладываем ординату, равную + a/ r₃, в том же масштабе (рис. 3.47 е), на правой опоре ординату, равную нулю. Соединяем эти две точки прямой. Из полученного графика в качестве линии влияния мы можем взять только правую часть - от опоры В до точки 13, где находился единичный груз Р = 1. Сносим на прямую точку 13 - правый узел разрезанной панели. Это правая ветвь линии влияния D_3-13. Для построения левой ветви единичный груз перемещаем на левую часть фермы и рассматриваем равновесие правой части. Составляем уравнение статики

∑М_К = 0;

- D_3-13 ·r₃ - R_В ·(a+ 6d)= 0.

Отсюда получаем D_3-13 =[ -(a+ 6d) · R_В]/ r₃. (3.42)

Строим график уравнения (3.42). На правой опоре откладываем ординату, равную -(a+ 6d)/ r₃ в том же масштабе, на левой - равную нулю. Соединяем эти две точки прямой. Сносим на нее узел 14 - левый узел разрезанной панели. Левая часть графика - это левая ветвь линии влияния D_3-13. Правую и левую ветви соединяем переходной линией. Построенная линия влияния D_3-13 показывает, что, когда груз справа от разреза, раскос растянут; когда слева - онсжат. Следует обратить внимание на эту особенность работы раскоса при перемещении груза по ферме.

Линия влияния усилия V_3-14. Проводим разрез П - П. Нетрудно видеть, что построение линии влияния усилия V_3-14 подобно построению линии влияния D_3-13. Моментная точка также «К». Рассматриваем равновесие левой части фермы

∑М_К = 0;

+ V_3-14 ·(a + d) - R_A · a = 0.

Отсюда V_3-14 = - a · R_A /(a + d). (3.43)

На левой опоре отложим ординату, равную -a /(a + d), на правой - равную нулю. Соединим эти две точки прямой, снесем на нее правый узел разрезанной нижней панели - узел 13. Это правая ветвь линии влияния V_3-14 (рис. 3.47 ж).

Рассматриваем равновесие правой части фермы ∑М_К = 0;

+ V_3-14 ·(a + d) - R_B /(a +6 d) = 0.

Отсюда V_3-14 =[(a +6 d) · R_B]/ (a + d). (3.44)

На правой опоре откладываем ординату, равную (a +6 d)/ (a + d), на левой - ординату, равную нулю. Соединяем эти две точки пря­мой, сносим на нее левый узел разрезанной нижней панели - узел 14. Это левая ветвь линии влияния V_3-14 . Стойка работает подобно раскосу - знак усилия в ней меняется при переходе груза с левой части фермы на правую.

Линия влияния усилия D_5-13. Разрез Ш-Ш (рис. 3.47 з). Единичный груз Р = 1 справа от разреза. Рассматриваем равновесие левой части фермы. Составляем уравнение статики ∑Y = 0; D_5-13 ·Cos α + R_A = 0.

ОтсюдаD_5-13 = - R_A / Cos α. (3.45)

Строим график уравнения (3.45). На левой опоре откладываем ординату, равную (- 1/ Cos α)_t на правой - ординату, равную нулю; соединяем точки прямой (рис. 3.47 з). Из графика можно взять только часть, соответствующую положению единичного груза Р = 1, т.е. от опоры В до узла 12. Сносим точку 12 - правый узел разрезаемой нижней панели на прямую. Получаем правую ветвь линии влияния усилия D_5-13.

Помещаем единичный груз Р = 1 слева от разреза Ш-Ш и рассматриваем равновесие правой части фермы ∑Y = 0; - D_5-13 ·Cos α + R_В = 0.

Отсюда D_5-13 = - R_В / Cos α. (3.46)

Строим график уравнения. Сносим левый узел разрезанной панели, т.е. точку 13. Получаем левую ветвь линии влияния. Ветви соединяем переходной прямой. Расставляем знаки. Как показывает построенная линия влияния (рис. 3.47 з), при перемещении груза от опоры А к опоре В усилие в раскосе меняет знак.

Линия влияния усилия V_5-12. С помощью разреза IV-IV вырежем узел 12 и рассмотрим его равновесие (рис. 3.47 а, к). Если единичный груз Р = 1 находится в узле 12, то V_5-12 = +1.

Если единичный груз Р = 1 находится в узле 13 и во всех левых узлах фермы, то V_5-12 = 0.

Если единичный груз Р = 1 находится в узле 11 и во всех правых узлах, то также V_5-12=0.

Строим линию влияния. Под узлом 12 откладываем ординату, равную + 1, под узлами 11, 13 - ординаты, равные нулю. Соединяем точки прямыми (рис. 3.47 и). Полученная линия влияния показывает, что при движении груза по ферме усилие в подвеске возникает только тогда, когда груз оказывается в узле 12. Если груз находится в других узлах фермы, подвеска не работает.

3.5.2. Построение линий влияния усилий в стержнях фермы с консолью.

Рассмотрим построение линий влияния усилий в стержнях фермы с консолью на примере рис 3.48 a.

1. При построении линий влияния усилий встержнях, находящихся в составе основного пролета А-В, нужно придерживаться следующего порядка. Первоначально, не обращая внимания на консольную часть фермы, начинают строить линии влияния как для обыч­ной балочной фермы на двух опорах по правилам,рассмотренным выше. Затем линии влияния продолжают до конца консоли (или консолей, если их две) по закону прямой. Правильность построения можно проверить статически, путем пробной постановки единичного гpyзa Р = 1 в узлах фермы и составления уравнений равновесия.

Для примера определим величину опорной реакции R_В при расположении единичного груза Р=1 в узле 10 консольной части фермы ∑М_А = 0:

-R_B·4d +1·7d =0.

Из этого равенства следует: R_B =1·7d/4d =7/4, что можно получить и графически на линии влияния R_B соединив прямой линией точку R_B =0 (под опорой А) с точкой R_B=1 (под опорой В) и продлевая эту прямую линию до конца консольной части фермы на графике получим под узлом 10 величину ординаты

R_B =7/4.

Напоминаем, что построению линий влияния должна предшествовать проверка фермы на статическую определимость и геометрическую неизменяемость.

2. Линии влияния усилий в стержнях, находящихся в составе консольной части фермы, строят, применяя метод разрезов и рассматривая равновесие отсеченной консольной части фермы при различных положениях единичного груза Р = 1 с помощью уравнений статики.

Единичный груз Р = 1 перемешаем по нижнему поясу фермы.

Линия влияния опорной реакции R_A. На левой опоре А откладываем ординату, равную +1, на правой опоре В - ординату, равную нулю. Соединяем эти две точки прямой. Затем продолжаем прямую до конца консоли С (рис. 3.48 б). Расставляем знаки. Знаки ординат линии влияния показывают следующее. Когда единичный груз находится в пределах пролета АВ, опорная реакция R_A направлена вверх, когда на консольной части ВС, - вниз.

Линия влияния опорной реакции R_В. Строим таким же образом (рис. 3.48 в). При всех возможных положе­ниях единичного груза Р = 1 на ферме опорная реакция R_В направлена вверх.

Линия влияния усилия U_15-16. Разрез I-I (рис. 3.48 а). Рассматриваем равновесие левой части фермы, единичный груз на правой части фермы. Моментная точка 3. На левой опоре А откладываем ординату, равную + d/h, на пра­вой опоре B - ординату, равную нулю. Соединяем две точки прямой, сносим на нее моментную точку. Соединяем сноску прямой с левой опорой. Правую ветвь линии влияния продолжаем до конца консоли. Расставляем знаки. Когда единичный груз находится на консоли, стержень U_15-16 сжат (рис. 3.48 г).

Линия влияния усилия D_3-15. Разрез I-I. Рассматриваем поочередно равновесие левой и правой частей фермы, соответственно перемещая единичный груз на правую и левую части. На левой опоре откладываем ординату, рав­ную (+ 1/Cos α), на правой (- 1/Cos α). Проводим две параллель­ные прямые. Сносим правый 15 и левый 16 узлы разрезанной панели. Соединяем полученные точки переходной прямой. Правую ветвь продолжаем до конца консоли. Расставляем знаки (рис. 3.48 д).

Линия влияния усилия U_12-13. Проводим разрез П-П. Моментная точка - 6. Когда единичный груз стоит в узле 13 (на опоре В) и слева от него, усилие равно нулю, т.е. стержень 12-13 не работает. Усилие в нем появится, когда единичный груз будет находиться справа от узла 13. Отбросим левую часть фермы и рассмотрим равновесие правой.

Единичный груз Р = 1 находится в узле 10.

Составим уравнение равновесия правой части фермы

∑М₆ = 0; + U_12-13 ·h + P ·3d = 0.

Отсюда U_12-13 = - 3d /h (при Р = 1). (3.47)

У конца консоли отложим ординату, равную (- 3d /h), и от ее вершины проведем прямую через точку 13. Все ординаты линии влияния U_12-13 отрицательны (рис. 3.48 е), т.е. стержень 12-13 при всех возможных положениях груза Р = 1 сжат.

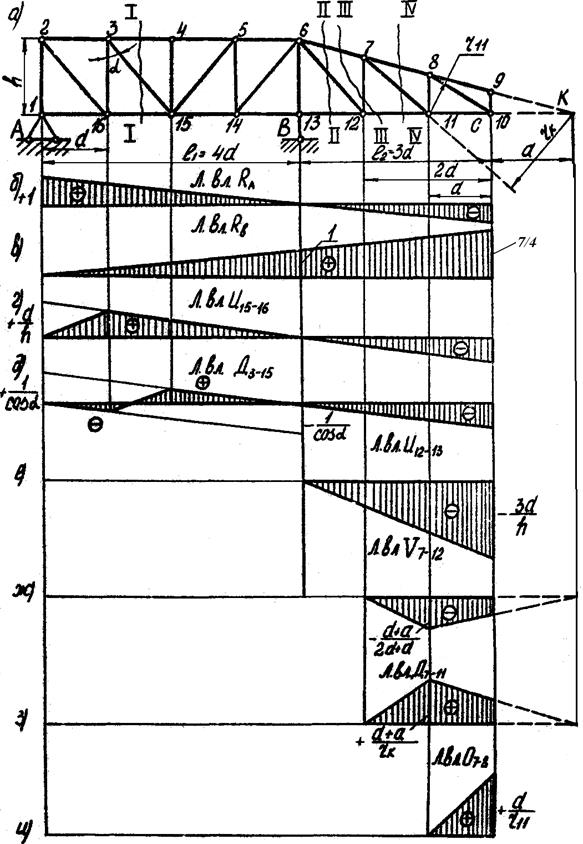
Рис. 3.48. Схема построения линий влияния усилий в стержнях фермы с консолью

Линия влияния усилия V_7-12. Проведем разрез Ш-Ш (рис. 3.48 а). Отбросим левую часть фермы. Моментная точка – «К». Определим величину усилия V_7-12 при различных положениях единичного груза.

Р = 1 находится в узле 12: усилие V_7-12 = 0.

Р = 1 находится в узле 11: ∑М_K = 0; - V_7-12 ·(2d + a) - P (d + a) = 0.

Отсюда V_7-12 = -(d + a) / (2d + a). (3.48)

Момент единичной силы Р = 1 изменяется по закону прямой, имеющей нулевую ординату (нулевое значение) под моментной точкой «К». Следовательно, величина усилия V_7-12 также будет иметь нулевое значение под точкой «К».

Под узлом 11 откладываем ординату, равную -(d + a) / (2d + a). Проводим прямую через вершину ординаты и точку с ординатой, равной нулю, под моментной точкой «К». Проводим вторую прямую через эту же вершину ординаты точку с ординатой, равной нулю, под узлом 13. Отбрасываем часть графика, находящегося за пределами фермы. Расставляем знаки. Все ординаты линии влияния отрицательны (рис. 3.48 ж).

Линия влияния усилия D_7-11. Разрез IV-IV. Строится аналогичным способом (рис. 3.48 з).

Все ординаты линии влияния положительные.

Линия влияния усилия О_7-8. Разрез IV-IV. Рассматриваем равновесие правой части фермы; единичный груз справа от разреза. Моментная точка - 11. Составляем уравнение равновесия

∑М₁₁ = 0;

1. Единичный груз Р = 1 в узле 11 О_7-8 = 0.

2. Единичный груз Р = 1 в узле 10. О_7-8 ·r₁₁ + P ·d = 0.

Отсюда О_7-8 = + d / r₁₁.

Строим линию влияния. Под узлом 10 откладываем ординату, равную + d / r₁₁, под узлом 11 - ординату, равную нулю. Соединяем точки прямой. Построенная линия влияния показывает, что стержень 7-8 растянут, когда единичный груз находится в узле 10, и не работает, когда единичный груз находится в узле 11 и во всех остальных левых узлах нижнего пояса фермы (рис. 3.48 и).