Пример расчета плоской фермы матричным методом

Для пояснения алгоритма расчета стержневых систем по методу МКЭ в матричной форме выполним расчет простейшей трехстержневой фермы, показанной на рис.3.52.

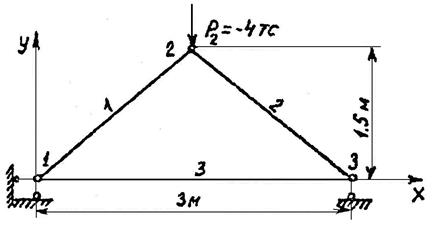
Рис.3.52. Схема плоской фермы

Построим структурную матрицу фермы (рис. 3.52) по ранее приведенной форме:

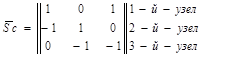
В построенной матрице:

строки – узлы фермы;

столбцы – стержни фермы.

Запишем матрицы – столбцы координат узлов фермы:

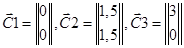
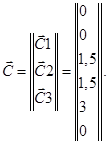
В матрице 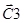цифра 3 обозначает координату узла 3 по оси Х (Х=3), вторая цифра 0 дает значение узла 3 по направлению оси Y (Y=0).

Транспонированная матрица 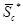путем замены строк столбцами при сохранении их нумерации будет иметь вид:

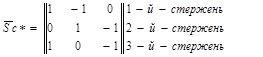
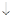
3-й узел

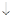
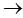
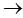2-й узел

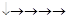1-й узел

Матрица проекций длин элементов фермы по формуле (3.51):

.

Длины стержней вычисляются по выражению (3.53):

;

;

.

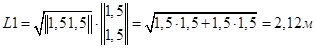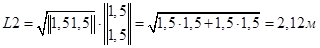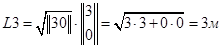Векторы направляющих косинусов стержней по формуле (3.54):

;

;

.

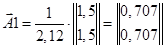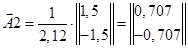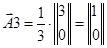Вектор внешних нагрузок по выражению (3.56):

.

Для получения из структурной матрицы 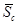матрицы 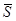произведем замену в матрице 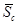значащих элементов 1 на соответствующие векторы направляющих косинусов (если элемент имеет значение (-1), то соответствующие векторы ставить с обратным знаком):

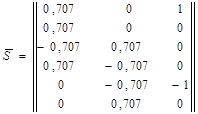
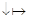3-й стержень с заменой 1 на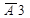

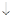
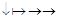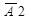
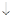
2-й стержень с заменой 1 на

1-й стержень с заменой 1 на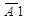

Для построения матрицы-вектора 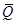из вектора внешних нагрузок 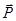удаляем первые две строки, т.к. узел 1 имеет закрепление (опору) по направлению Х (первая строка) и по направлению Y (вторая строка), а также удаляем строку 6 как закрепление узла 3 по направлению Y. В результате получим матрицу-вектор 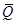следующего вида:

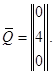
Для построения матрицы 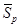из матрицы 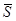аналогично построению матрицы-вектора Q удаляем первую, вторую и шестую строки:

= .

Решение уравнений (3.59) и (3.60) в матричной форме дает следующий результат:

,

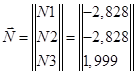где N1, N2 и N3 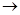усилия в стержнях 1, 2 и 3 [Tc].