Статически определимые плоские фермы

Общие сведения

Фермой называется стержневая конструкция, предназначенная, как и обычная балка сплошного сечения, для перекрытия пролетов. В реальных фермах стержни соединяются в узлах с помощью болтов, заклепок или сварных швов. Узлы в таком исполнении жесткие. Расчет ферм с учетом жесткости узлов чрезвычайно сложен. Поэтому на практике к нему не прибегают. Фермы рассчитывают по более простым расчетным схемам, заменяя реальные жесткие узлы на идеальные шарниры. Такая замена, собственно упрощая расчеты, вполне допустима в практике проектирования, так как сохраняет неизменными все отличительные особенности ферм и не искажает результаты расчетов.

К основной особенности ферм относится работа всех стержней только на продольные усилия (растяжение и сжатие) при условии, которое является нормой, что нагрузки к фермам приложены только в узлах.

Если по заданию на проектирование нагрузки к ферме приложе­ны в промежуточных точках стержней, их все-таки перераспределя­ют на смежные узлы.

Стержни ферм прямолинейны. К составным частям фермы относятся: верхний пояс (в статике сооружений «О»), нижний пояс «U» и решетка (рис. 3.29 а). Вертикальные стержни решетки называются стойками или подвесками «V», наклонные - раскосами «Д».

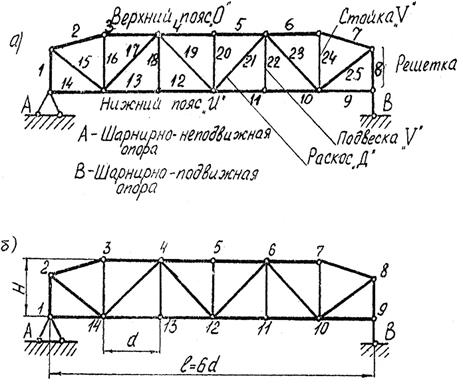
Рис. 3.28. Схема фермы с наименованиями характерных стержней:

а - схема фермы с произвольно выбранной последовательностью нумерации стержней; б - схема фермы с произвольно выбранной последовательностью нумерации узлов, координаты (Х, Y) каждого узла определяют в выбранной системе (обычно начало координат помещают в узле 1 на неподвижной опоре)

Каждому узлу фермы дадим собственный порядковый номер: 1, 2, 3 и т.д. Это даст возможность однозначно определить каждый стержень фермы. Например, левый крайний стержень нижнего пояса имеет обозначение U_1-14, правый крайний стержень верхнего пояса - О_7-8, и т.д. (рис. 3.28, б). Пролет фермы «L» - это расстояние между крайними опорными узлами пояса, высота фермы Н - наибольшее расстояние между -поясами по вертикали. Стержни нижнего пояса называются так­же панелями, длина панелей «d» в большинстве случаев принимается одинаковой, рис. 2.28 б. При расчетах с применением ЭВМ необходимо каждому стержню присвоить индивидуальный цифровой номер начиная с первого.

По очертанию поясов различают фермы с параллельными поясами (рис. 3.29 а), треугольные фермы (рис. 3.29 б), с криволинейными (одним или обоими поясами (рис. 3.29 в, г) (по кривой располагаются только узлы пояса, сами стержни прямые). Наиболее рационально очертание криволинейного пояса по параболе.

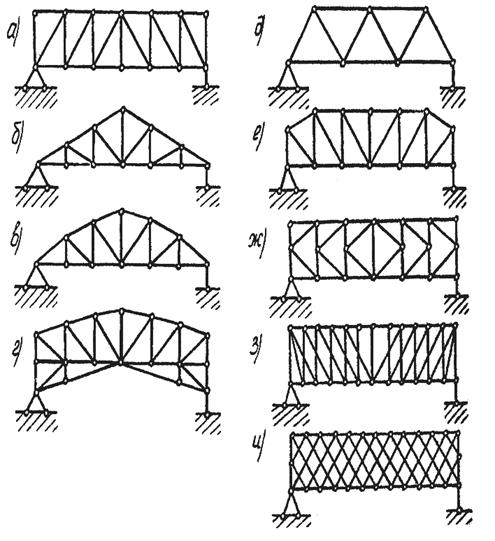
Рис.3.29. Типовые схемы ферм:

а - с параллельными поясами; б - треугольная ферма; в - с криволинейным поясом; г - с двумя криволинейными поясами; д - с треугольной системой решетки; е - с раскосной системой решетки; ж - с полураскосной системой решетки; з - с многораскосной системой решетки; и - многорешетчатая система

Опоры

В курсе строительной механики рассматривается расчет геомет­рически неизменяемых систем (сооружений), т. е. таких, перемеще­ния отдельных точек которых возможны только в результате дефор­мации систем. Неподвижность таких систем (их геометрическая неизменяемость) относительно земли¹обеспечивается опорными связями (опорами). В опорах возникают реакции, которые вместе с заданными нагрузками представляют уравновешенную систему внешних сил, действующих на сооружение. Рассмотрим различные типы опор плоских систем.

Первый тип опоры представлен на рис. 3.30. Он состоит из двух балансиров - верхнего 1 и нижнего 3, между которыми проложен валик 2, играющий роль цилиндрического шарнира ².

¹ Под термином «земля» понимается геометрически неизменяемая система -диск.

² В дальнейшем при расчете плоских систем цилиндрический шарнир будем называть шарниром.

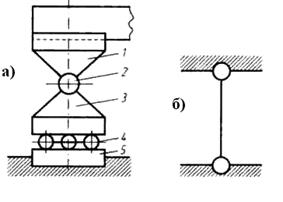
Рис. 3.30. Шарнирно подвижная опора (а) и ее схематическое изображение (б):

1 – верхний балансир; 2 – валик; 3 – нижний балансир; 4 – опорные катки; 5 – опорная подушка

Благодаря валику (2) верхний балансир может поворачиваться относительно нижнего. Кроме того, он может вместе с нижним балансиром, опирающимся на катки 4, перемещаться по опорной плоскости, называемой опорной подушкой 5.

Следовательно, рассматриваемая опора имеет две степени свободы (изменяемости). Трением, развивающимся в опоре, принято при расчете пренебрегать, а потому реакция такой опоры представляет собой силу, проходящую через центр шарнира и перпендикулярную направлению возможного перемещения катков, т. е. верхней плоскости опорной подушки. Эта сила определяется одним параметром - ее величиной. Рассматриваемая опора носит название цилиндрической подвижной, или шарнирно-подвижной. Схематически ее изображают в виде одного стержня с двумя идеальными (без трения) шарнирами на концах (рис. 3.30 б).

Стержень, схематически изображающий шарнирно-подвижную опору, условно принимается бесконечно длинным; верхняя точка такого стержня может перемещаться лишь по прямой линии (прямая есть окружность бесконечно большого радиуса), перпендикулярной его оси, что полностью соответствует тем условиям, в которых на­ходится действительная шарнирно-подвижная опора. Собственные деформации опоры при расчетах не учитываются, т. е. опорный стержень условно считается бесконечно жестким.

Второй тип опоры (рис. 3.31) отличается от первого тем, что ниж­ний балансир (3)закреплен и не может перемещаться. Такая опора обладает одной степенью свободы и носит название цилиндрической неподвижной или шарнирно-неподвижной. Реакция ее представляет собой силу, проходящую через центр шарнира. Эта сила может иметь любое направление и определяется, следовательно, двумя параметрами - величиной и на­правлением (или, что то же самое, величинами двух составляющих ее сил, например, вертикальной и горизонтальной).

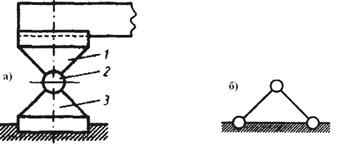
Рис. 3.31. Шарнирно- неподвижная опора (а) и ее схематическое изображение (б): 1 – верхний балансир; 2 – валик; 3 – нижний балансир

Схематически опора второго типа изображается с помощью двух стержней с идеальными шарнирами по концам; верхний шарнир является общим для обоих стержней (рис. 3.31 б). Такая схема определяет точку приложения опорной реакции (центр верхнего шарнира), оставляя ее направление неизвестным.

Направления стержней на схеме шарнирно-неподвижной опоры могут быть выбраны вполне произвольно, так как силу (реакцию) можно разложить на два любых направления.

Третьим типом опоры является так называемая защемляющая неподвижная опора, или заделка (рис. 3.32), степень свободы которой равна нулю.

Реакция опоры третьего типа определяется тремя параметрами, например: величиной и направлением силы, проходящей через произвольную точку, и моментом относительно этой точки. Эту реакцию можно представить как сочетание реактивного момента в заделке (опорном сечении) с реакцией шарнирно-неподвижной опоры.

Схематически опора третьего типа может быть представлена тремя стержнями (рис. 2.32 б); для того, чтобы заделку можно было считать абсолютно жесткой, расстояние l₀ должно быть очень малым или брус на участке длиной l₀ надо рассматривать как бесконечно жесткий.

Отметим, что число стержней в схематическом изображении любой опоры всегда равняется числу параметров, определяющих полную реакцию этой опоры.

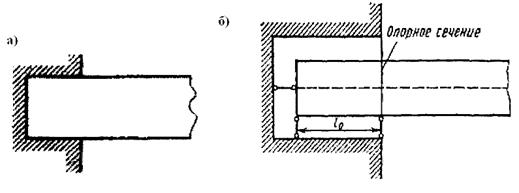
Рис. 3.32. Защемляющая неподвижная опора (заделка) (а) и схематическое изображение опорных стержней (б)