АЛГОРИТМ МЕТОДА ГАУССА

Решение системы n линейных алгебраических уравнений вида А∙х = bпо этому алгоритму состоит из двух этапов.

На первом этапе (прямой ход) исходная система за n однотипных шагов преобразуется таким образом, что матрица коэффициентов преобразованной системы становится верхней треугольной, т. е. все элементы, расположенные ниже ее главной диагонали, равны нулю.

На втором этапе (обратный ход) последовательно определяются значения неизвестных от х_n до x₁.

Последовательность операций, выполняемых при прямом ходе:

На первом шаге в исходной системе уравнений

a₁₁х₁ + а₁₂х₂ + … + а₁_nx_n = b₁

a₂₁х₁ + а₂₂х₂ + … + а₂_nx_n = b₂

……………………………..

a_n₁х₁ + а_n₂х₂ + … + а_nnx_n = b_n

первое уравнение делится на a₁₁. Далее х₁ исключается из всех последующих уравнений (i = 2, ..., n) путем умножения первого уравнения каждый раз на а_i₁ и вычитания из i-гo уравнения. В результате этих операций получается система уравнений с матрицей коэффициентов А⁽¹⁾:

х₁ + а₁₂⁽¹⁾х₂ + … + а₁_n⁽¹⁾x_n = b₁⁽¹⁾

0 + а₂₂⁽¹⁾х₂ + … + а₂_n⁽¹⁾x_n = b₂⁽¹⁾

……………………………..

0 + а_n₂⁽¹⁾х₂ + … + а_nn⁽¹⁾x_n = b_n⁽¹⁾

где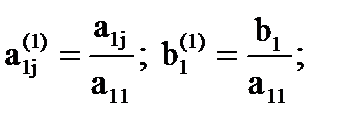

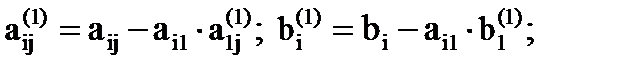где i, j = 2, …, n.

Выполнение операций первого шага требует, чтобы элемент а₁₁, называемый ведущим, был отличен от нуля.

Второй шаг состоит в исключении x₂ из уравнений 3, ..., n, полученной на первом шаге системы путем выполнения аналогичных операций при использовании в качестве ведущего элемента а₂₂⁽¹⁾ В результате система приводится к виду А⁽²⁾∙х = b⁽²⁾.

Третий и последующий шаги выполняются аналогично.

На k-м шаге элементы матрицы A⁽^k⁾ и столбца b⁽^k⁾ определяются по выражениям:

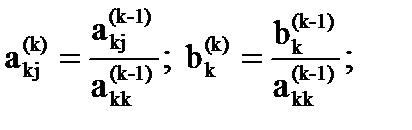
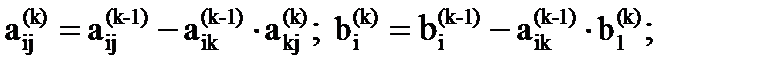
i, j = k + 1, …, n.

При прямом ходе ведущими элементами последовательно выступают а₁₁, а₂₂⁽¹⁾, а₃₃⁽²⁾, …, а_nn⁽ⁿ^-1) и их отличие от нуля является условием осуществимости процесса вычислений.

В результате выполнения n шагов образуется система уравнений вида

х₁ + а₁₂⁽¹⁾х₂ +…+ а₁₍_n_-2)⁽¹⁾х_n_-2 + а₁₍_n_-1)⁽¹⁾х_n_-1 + а₁_n⁽¹⁾х_n = b₁⁽¹⁾

х₂ +…+ а₁₍_n_-2)⁽²⁾х_n_-2 + а₁₍_n_-1)⁽²⁾х_n_-1 + а₁_n⁽²⁾х_n = b₁⁽²⁾

………………………………………………………….

х_n_-2 + а₍_n_-2)(_n_-1)⁽ⁿ^-2)х_n_-1 + а₍_n_-2)_n⁽ⁿ^-2)х_n = b_n_-2⁽ⁿ^-2)

х_n_-1 + а₍_n_-1)_n⁽ⁿ^-1)х_n = b_n_-1⁽ⁿ^-1)

х_n = b_n⁽ⁿ⁾

На этапе обратного хода определяются искомые неизвестные от х_n до х₁.

<1 2 345 6 7 >

Дата добавления: 2018-09-24; просмотров: 359;