ИСПОЛЬЗОВАНИЕ МЕТОДА LU-РАЗЛОЖЕНИЯ В РЕШЕНИИ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ ЗАДАЧ

Определение.Допустим, что матрица A представляется в виде произведения двух матриц:

А = LU. (1.1)

Представление (1.1) матрицы A называется LU-разложением матрицы А, если U – верхняя треугольная матрица, все диагональные элементы которой равны единице, а L – нижняя треугольная матрица, все диагональные элементы которой не равны нулю.

Обозначения матриц L и U соответствуют английским словам: lower – нижний, upper – верхний.

Для решения системы уравнений АХ=В необходимо:

а) матрицу A представить в виде произведения нижней треугольной L и верхней треугольной U матриц (триангулировать A=LU), записав уравнение LUX=B;

б) решение системы уравнений сводится к двухфазовой операции с треугольными матрицами:

- решению LY=B относительно Y;

- решению UX=Y относительно X.

Для LU-разложения исходной матрицы используется множество алгоритмов. В данной лабораторной работе применяется достаточно простой алгоритм последовательного определения элементов матриц L и U:

Пусть матрица A имеет размерность n × n.

1 шаг. Определение первого столбца матрицы L и первой строки матрицы U.

Принимается значение k = 1, тогда искомые элементы матриц L и U определяются по выражениям:

L_i,k = A_i,k, где i = n..1;

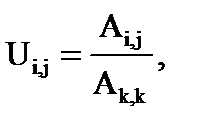где i = 1, j = n..1.

Далее необходимо пересчитать элементы исходной матрицы A при i = n..2, j = n..2 по выражению

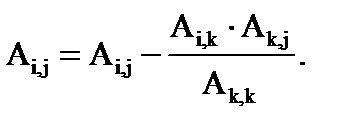(1.2)

2 шаг.Определение второго столбца матрицы L и второй строки матрицы U.

Принимается значение k = 2, тогда искомые элементы матриц L и U определяются по выражениям:

L_i,k = A_i,k при i ≥ k и L_i,k = 0 при i < k, где i = n..1;

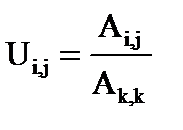при j ≥ k и U_i,j = 0 при i < k, где i = 2, j = n..1.

Далее необходимо пересчитать элементы исходной матрицы A при i = n..3, j = n..3 по выражению (1.2).

s шаг.Определение s-ого столбца матрицы L и s-ой строки матрицы U.

Принимается значение k = s, тогда искомые элементы матриц L и U определяются по выражениям:

L_i,k = A_i,k при i ≥ k и L_i,k = 0 при i < k, где i = n..1;

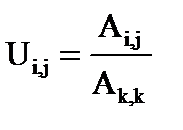при j ≥ k и U_i,j = 0 при i < k, где i = s, j = n..1.

Далее необходимо пересчитать элементы исходной матрицы A при i = n..s+1, j = n.. s+1 по выражению (1.2).

Количество шагов равно размерности исходной матрицы.