ВЕКТОРЫ. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. ДЛИНА ВЕКТОРА. ОРТОГОНАЛЬНЫЕ ВЕКТОРЫ

Если матрица состоит только из одного столбца (j = 1), то такой объект называется вектором-столбцом. Если матрица состоит только из одной строки (i = 1), то такой объект называется вектором-строкой. Примеры смотри в вопросе 3.

При анализе данных важно понимать, с какими векторами мы имеем дело – со столбцами или строками. Так, например, значения напряжения снятые в одном узле электрической сети можно рассматривать как вектор-строку. Тогда как показания приборов во всех узлах сети в определенный момент времени будут рассматриваться как вектор-столбец.

Всякий вектор-столбец транспонированием превращается в вектор-строку.

В тех случаях, когда форма вектора не оговаривается специально, а просто говорится вектор, имеется в виду вектор-столбец.

Нулевым вектором называется вектор, все элементы которого равны нулю.

Векторы можно складывать и умножать на числа так же, как это делается с матрицами.

Два вектора x и у называются коллинеарными, если существует такое число а, что ах = у.

Два вектора одинаковой размерности можно перемножать. Пусть имеется два вектора х = (х₁, х₂, ..., х_n)^t иу = (у₁, у₂, ..., у_n)^t. Руководствуясь правилом перемножения «строка на столбец», мы можем составить из них два произведения: х^tу и ху^t.

Первое произведение называется скалярным или внутренним. Его результат – это число. Для него также используется обозначение (х,у).

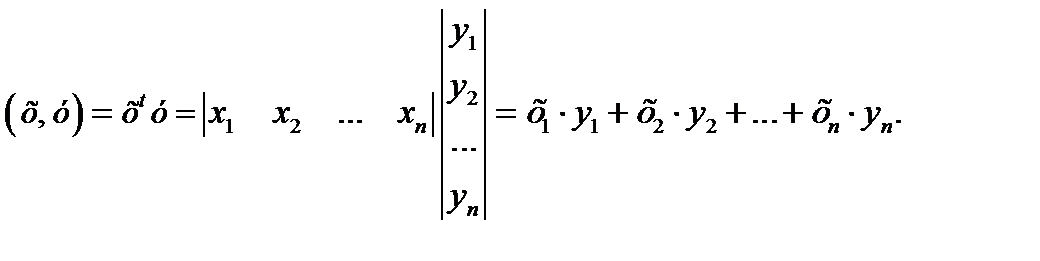
Второе произведение называется внешним. Его результат – это квадратная матрица размерности n.

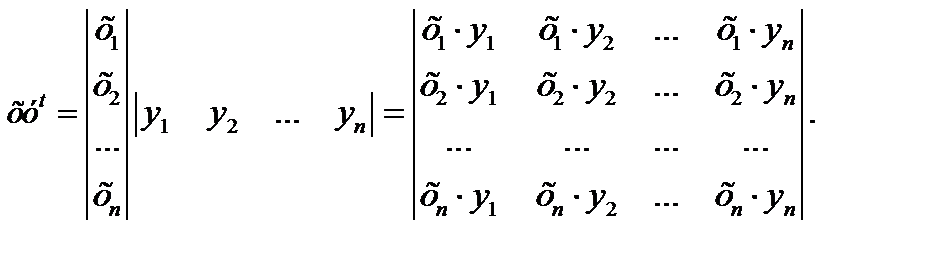
Векторы, скалярное произведение которых равно нулю, называются ортогональными.

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина определяет квадрат длины вектора х.

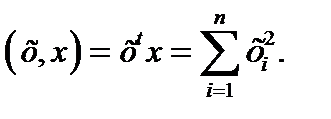
Для обозначения длины вектора (нормы вектора) используется обозначение

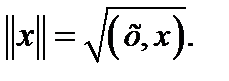
Вектор единичной длины называется нормированным. Ненулевой вектор можно нормировать, разделив его на длину.

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.