РАСЧЕТ ТОКОВ КОРОТКОГО ЗАМЫКАНИЯ В ЭЛЕКТРИЧЕСКОЙ СИСТЕМЕ НА ОСНОВЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ

Для электрической системы любой сложности выполняется закон Ома, записанный в матричной форме

U = IR или YU = I.

Для расчета токов КЗ в электрической системе удобнее пользоваться формулой через проводимости. В этом случае Y – это квадратная матрица собственных и взаимных проводимостей электрической сети, размерность которой зависит от общего количества узлов; U – это вектор-столбец напряжений в узлах сети; I – это вектор-столбец токов в ветвях схемы.

Вектор напряжений содержит известные составляющие E_i– напряжения источников питания (электростанций) и неизвестные составляющие U_i. Если узел соответствует точке КЗ, то напряжение в этом узле равно 0.

Вектор токов также можно разбить на составляющие токов от источников питания I_г (генераторов) и ток КЗ I_к – ток в поврежденном узле. В остальных узлах ток будет равен нулю, т.к. по первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи равна нулю.

Для задач большой размерности все три матрицы разбиваются на блоки, в которых условно выделяются генерирующие узлы, поврежденные узлы и промежуточные (остальные) узлы. В матричном виде это будет выглядеть следующим образом

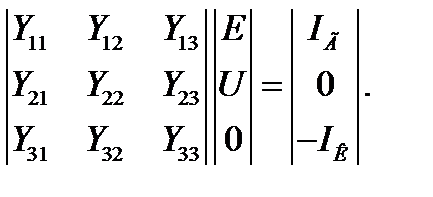
В этой системе уравнений известна матрица проводимостей, т.к. это структурный параметр, и Е – напряжения источников. U и I – это режимные параметры. Представим полученное матричное выражение в виде 3 уравнений с 3 неизвестными:

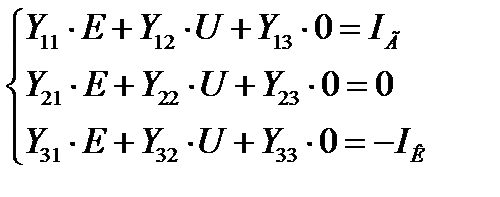
Выразим из каждого уравнения неизвестные

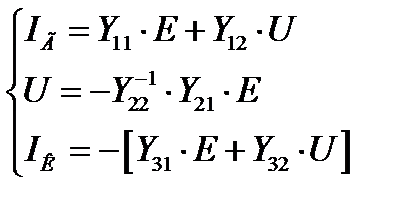
Решив второе уравнение, определим напряжения в узлах сети. Подставив полученные значения U, определим генерирующие токи из первого уравнения и ток КЗ из третьего уравнения.