ФАКТОРИЗАЦИЯ КВАДРАТНОЙ МАТРИЦЫ

В математике факторизация – это декомпозиция объекта (например, числа, полинома или матрицы) в произведение других объектов или факторов, которые будучи перемноженными, дают исходный объект.

Матрица может быть факторизована на произведение матриц специального вида. Одним из основных примеров этого является использование ортогональных, унитарных и треугольных матриц. Существуют различные способы факторизации: LU-разложение, LH, QR и т.д.

Использование метода LU-разложения для решения систем линейных алгебраических уравнений рассмотрено в вопросе 7.

Двойная факторизация – представление обратной матрицы в виде произведения элементарных верхних и нижних треугольных матриц, в которых не равны нулю все элементы только одной строки или одного столбца. Такие матрицы называются факторными.

Произведение факторных матриц дает обратную матрицу.

Рассмотрим структуру факторных матриц:

1) Левая факторная матрица на к-м шаге факторизации L_k.

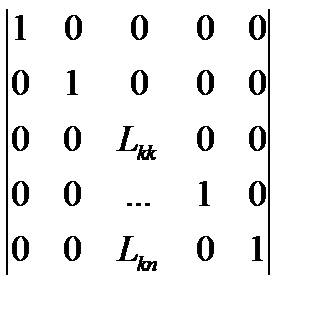
Элементарная нижняя треугольная матрица, в которой диагональные элементы равны 1, в к-ом столбце диагональные и все поддиагональные элементы не равны нулю. Все остальные элементы матрицы равны нулю. Таких матриц может быть n.

Элементы этой матрицы определяются по формулам:

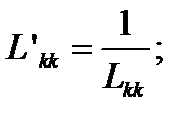(1)

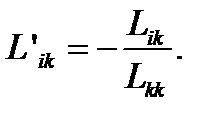(2)

2) Правая факторная матрица R_к.

Это элементарная верхняя треугольная матрица с единичной диагональю.

В к-ой строке элементы, лежащие правее диагонали, не равны нулю. Все остальные элементы матрицы равны нулю.

Таких матриц может быть n-1. Элементы матрицы R вычисляются по формуле:

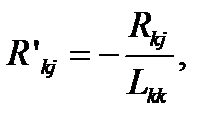(3)

k=1…n, j=k+1…n, i=k+1…n.

Для квадратной матрицы А размерностью (n x n) существует n левых и (n-1) правых факторных матриц, таких, что их произведение дает обратную матрицу:

A^-1= R₁∙ R₂∙ …∙ R_n-1∙ L_n∙ L_n-1∙ …∙ L₁. (4)

Здесь: А – исходная матрица; L – левые факторные матрицы, полученные на 1, 2, …, n шагах факторизации; R – правые факторные матрицы.

Существует эффективные алгоритмы перемножения факторных матриц, в которых нулевые элементы и единицы на диагонали не хранятся, а подразумеваются в ходе вычислений. В памяти хранятся и участвуют в вычислениях только значащие элементы матриц.

Решение ищем в виде:

АХ = В;

Х = А^-1∙В.

Алгоритм факторизации:

1) Выбор очередного ведущего элемента а_кк, определяющего опорную строку и опорный столбец;

2) На основе элементов опорной строки и опорного столбца пересчитываются все остальные элементы матрицы по формуле:

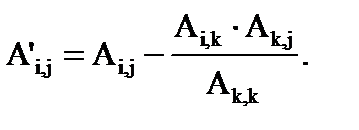(5)

3) Пересчитываем элементы опорного столбца по формуле (1);

4) Пересчитываем элементы опорной строки по формуле (3);

5) Пересчитываем ведущий элемент по формуле (2) L₁ … L_к … L_n

6) Если таким образом получены n левых и (n-1) правая факторная матрица, то переходим к пункту 7, иначе – возврат к пункту 1;

В результате все поле матрицы будет заполнено элементами факторных матриц L и R. Полученная матрица называется факторизованной;

7) Расчет обратной матрицы А^-1 перемножением факторных матриц по формуле (4);

8) Решение системы уравнений по формуле: Х = А^-1∙В.