ПРИМЕНЕНИЕ МЕТОДА НЬЮТОНА ПРИ РЕШЕНИИ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ ЗАДАЧ

Метод Ньютона является одним из наиболее эффективных методов решения самых разных нелинейных задач.

Пусть дана исходная система нелинейных уравнений:

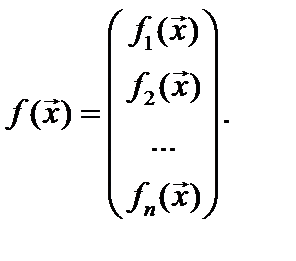(1)

Чтобы привести расчетную формулу метода Ньютона, через 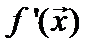обозначим матрицу Якоби:

(2)

Итерационная формула метода Ньютона для вычисления корней нелинейной системы уравнений (1) имеет вид:

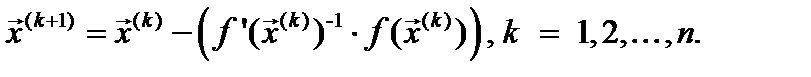(3)

Формула (3) предполагает использование трудоемкой операции обращения матрицы, поэтому непосредственное ее использование для вычисления 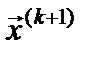не всегда целесообразно. Преобразуем (3) следующим образом. Перенося 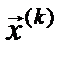влево и умножая результат на 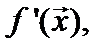получаем эквивалентную системе (2) систему линейных алгебраических уравнений

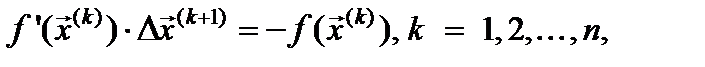(4)

относительно разности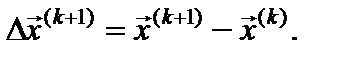

Решив систему линейных алгебраических уравнений (4) каким-либо приемлемым методом, вычисляем очередное приближение к корню

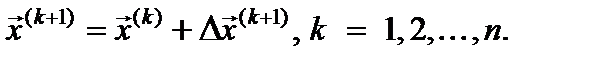(5)

Если 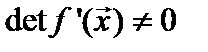в достаточно малой окрестности корня системы (1), то в этой окрестности метод Ньютона сходится, причем с квадратичной скоростью, т.е. если 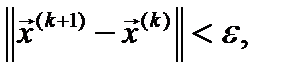то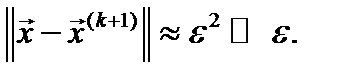

Квадратичная скорость сходимости метода Ньютона позволяет использовать простой практический критерий окончания итерационного процесса

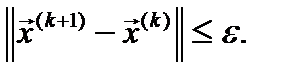(6)

Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро.