Векторы магнитного поля

Магнитное поле характеризуется векторами: магнитной индукцией 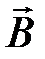, вектором намагниченности вещества 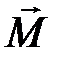, и вектором напряжённости магнитного поля .

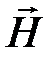Магнитная индукция ― векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся электрически заряженную частицу со стороны магнитного поля.

Сила, действующая на движущийся заряд равна:

.

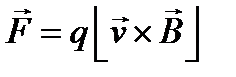Здесь q ― электрический заряд; v ― скорость.

Направление силы 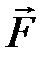находят по правилу векторного произведения (рис.1.2).

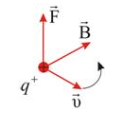
Рис. 1.2. Сила Лоренца

Сила 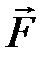максимальна, если вектор скорости 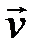перпендикулярен вектору индукции 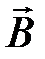.В этом случае

.

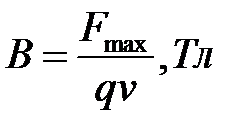Итак, магнитная индукция равна отношению силы, действующей на электрически заряженную частицу, к произведению заряда и скорости частицы, если направление скорости таково, что эта сила максимальна, и имеет направление, перпендикулярное к векторам силы и скорости, совпадающее с поступательным перемещением правого винта при вращении его от направления силы к направлению скорости частицы с положительным зарядом.

Магнитное поле действует, не только на отдельные движущиеся

заряды, но и на проводники, по которым течет электрический ток (рис.1.3).

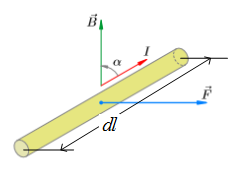
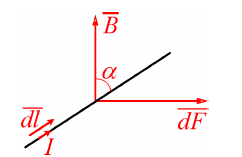
Рис.1.3. Проводник с током в магнитном поле

Например, сила 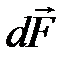, с которой однородное магнитное поле действует на элемент dl тонкого проводника с токм I равна

,

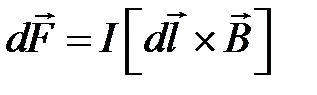где вектор 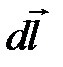направлен понаправлению тока в проводнике.

Направление силы d F → {\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки. Модуль силы Ампера можно найти по формуле:

d F = I B d l sin ⁡ α , {\displaystyle dF=IBdl\sin \alpha ,} ,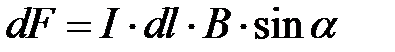

где α {\displaystyle \alpha }a — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Полная сила F , действующая на проводник длиной l с током I, составит

.

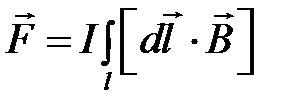Если проводник прямолинейный, а индукция B на оси проводника по-

стоянна и перпендикулярна направлению тока I, то модуль вектора си-

лы может быть рассчитан следующим образом

/

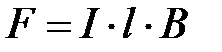
Направление силы d F → {\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки. Модуль силы Ампера можно найти по формуле:

d F = I B d l sin ⁡ α , {\displaystyle dF=IBdl\sin \alpha ,} ,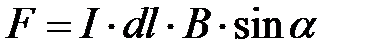

где α {\displaystyle \alpha }a — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Величина индукции зависит от свойств среды. Под действием магнитного поля вещество может намагничиваеться. В этом случае появляется дополнительное поле, которое налагается на первичное поле. Намагничивание характеризуется намагниченностью.

Намагниченность ( 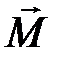) ―векторная величина, равная сумме магнитных моментов атомов в единице объема вещества: .

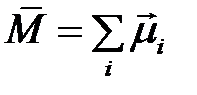Вектор 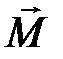измеряется в амперах на метр (А/м).

При рассмотрении многих процессов удобно ввести вектор напряженности магнитного поля.

Напряжённость магнитного поля ― векторная величина, равная геометрической разности магнитной индукции, деленной на магнитную постоянную, и намагниченности.

.

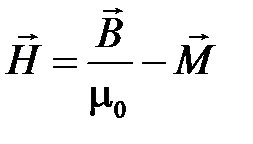Намагниченность связана с 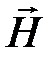соотношением:

,

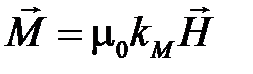где 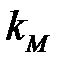― магнитная восприимчивость, характеризует свойство вещества намагничиваться в магнитном поле.

С вектором магнитной индукции напряжённость магнитного поля 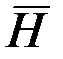связана соотношением:

,

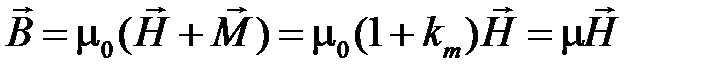где μ = μ₀ μ_r ― абсолютная магнитная проницаемость;

μ₀ = 4π∙10^-7 Гн/м ― магнитная постоянная;

μ_r ― относительная магнитная проницаемость.