Принцип непрерывности магнитной индукции
Поток вектора магнитной индукции  сквозь любую замкнутую поверхность
сквозь любую замкнутую поверхность 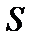 равен нулю:
равен нулю:
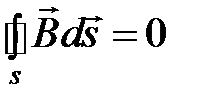 . (1.3)
. (1.3)
Перейдем к дифференциальной форме записи уравнения (1.3), используя теорему Остроградского–Гаусса:
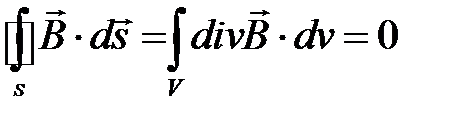 .
.
Отсюда имем принцип непрерывности магнитной индукции в дифференциальной форме:
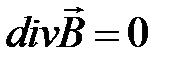 или
или 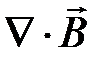 . (1.4)
. (1.4)
В декартовой системе координат уравнение (1.4) записывается
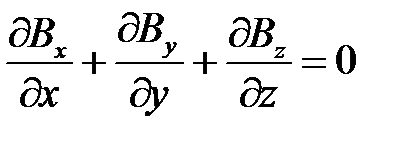 .
.
Теорема Гаусса (постулат Максвелла)
В интегральной форме.
Поток вектора электрической индукции (вектора электрического смещения) 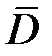 сквозь произвольную замкнутую поверхность
сквозь произвольную замкнутую поверхность 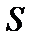 равен алгебраической сумме свободных зарядов, расположенных в объеме, ограниченном этой поверхностью (рис. 1.8):
равен алгебраической сумме свободных зарядов, расположенных в объеме, ограниченном этой поверхностью (рис. 1.8):
 , (1.5)
, (1.5)

Рис.1.8. Электрическое поле объёмного заряда
Теорему Гаусса Максвелл обобщил (постулировал) и на переменные электрические поля.
Левую часть уравнения (1.5) преобразуем по теореме Остроградского‒Гаусса:
 .
.
Отсюда имеем теорему Гаусса в дифференциальной форме:
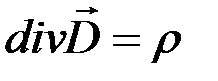 . (1.6)
. (1.6)
В декартовой системе координат уравнение (1.6) записывается
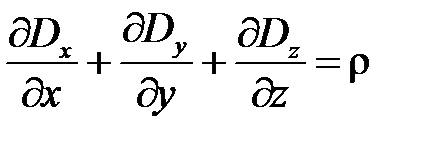 .
.
Дата добавления: 2017-08-01; просмотров: 938;
