Уравнения Максвелла

Закон полного тока

В интегральной форме.

Циркуляция напряженности магнитного поля по любому замкнутому контуру равна полному току сквозь поверхность, ограниченную этим контуром (рис.1.4):

.

Рис. 1.4. Контур в магнитном поле

Левую часть уравнения преобразуем по теореме Стокса:

.

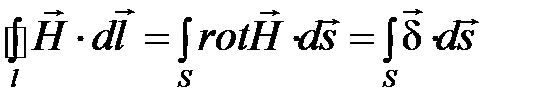Отсюда имеем дифференциальную форму закона полного тока:

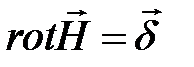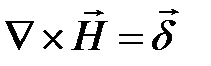или , (1.1)

где 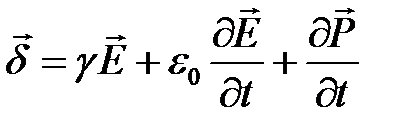― вектор плотности полного тока ;

―оператор пространственного дифференцирования ― оператор на́бла (оператор Гамильтона).

В декартовой системе координат и операция 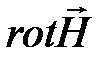записыватся так:

.

Для наглядного представления о роторе вектора 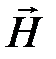на рис.1.3 изображены линии магнитного поля цилиндра с током плотностью δ. Эти линии ― концентрические окружности ― показывают, что поле вихревое.

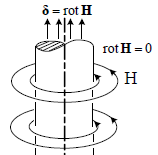
Рис.1.5. Цилиндрический проводник с током

.

Уравнение (1.1) представляет векторную запись трех уравнееий: .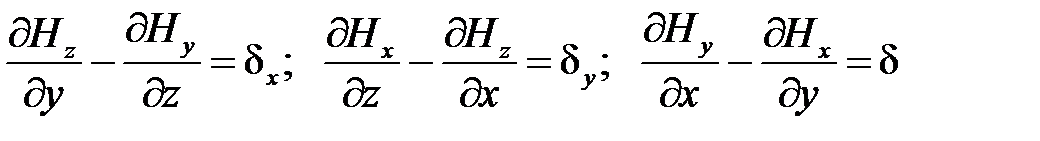

Из закона полного тока видно, что магнитное поле порождается не только движущими зарядами (ток проводимости, ток переноса и ток поляризации), но и изменяющимся электрическим полем.

Возьмем операцию div от левой и правой части выражения закона полного тока:

.

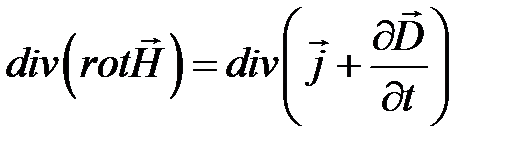Учитывая, что , получаем

уравнение непрерывности плотности полного тока: