Векторное произведение двух векторов.
Векторным произведением двух векторов 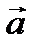 и
и 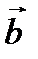 с углом
с углом 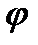 между ними называется вектор
между ними называется вектор 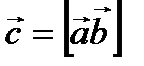 , который определяется следующим образом:
, который определяется следующим образом:
1. 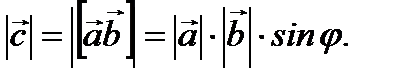 (2.18)
(2.18)
2. Вектор 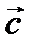 перпендикулярен плоскости, которая проходит через векторы
перпендикулярен плоскости, которая проходит через векторы 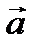 и
и 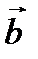 , и направлен так, что с его конца кратчайший поворот от
, и направлен так, что с его конца кратчайший поворот от 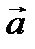 к
к 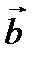 виден против хода часовой стрелки (рис. 2.8).
виден против хода часовой стрелки (рис. 2.8).
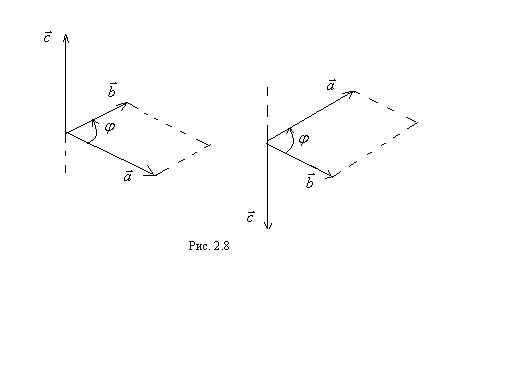
Из определения векторного произведения следует, что если в нем менять местами векторы, то направление векторного произведения изменится на противоположное, то есть 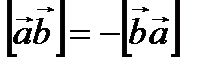 (рис. 2.8). Как видно из (2.18), модуль векторного произведения
(рис. 2.8). Как видно из (2.18), модуль векторного произведения 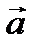 и
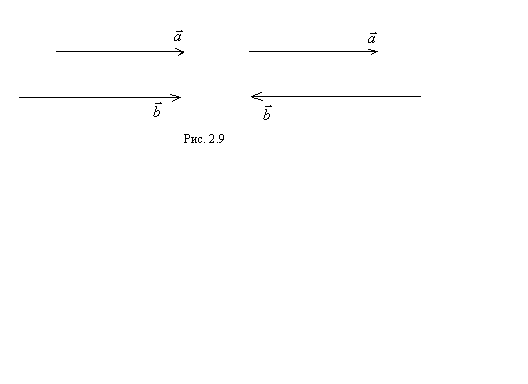
и 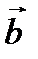 равен площади параллелограмма, построенного на этих векторах, как на сторонах (геометрический смысл векторного произведения двух векторов). Заметим, что параллельные векторы называются коллинеарными (рис. 2.9).
равен площади параллелограмма, построенного на этих векторах, как на сторонах (геометрический смысл векторного произведения двух векторов). Заметим, что параллельные векторы называются коллинеарными (рис. 2.9).
Теорема 2.2.Равенство нулю векторного произведения двух не нулевых векторов 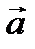 и
и 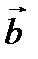
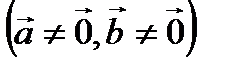 является необходимым и достаточным условием коллинеарности векторов
является необходимым и достаточным условием коллинеарности векторов 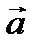 и
и 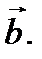
Доказательство:
Необходимость. Дано, что векторы 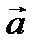 и
и 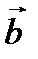 коллинеарны. Доказать, что
коллинеарны. Доказать, что 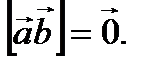
Из условия теоремы следует, что угол между векторами 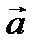 и
и 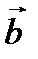
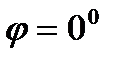 или
или 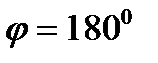 . Но
. Но 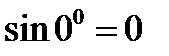 и
и 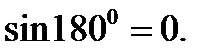 Тогда согласно (2.18)
Тогда согласно (2.18) 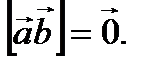
Достаточность. Дано, что 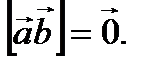 Доказать, что векторы
Доказать, что векторы 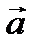 и
и 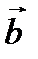 коллинеарны.
коллинеарны.
Из условия теоремы имеем 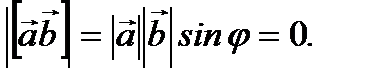 Но так как
Но так как 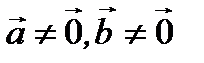 , то
, то 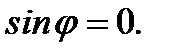 Тогда
Тогда 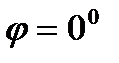 или
или 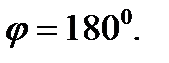 А это означает, что векторы
А это означает, что векторы 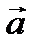 и
и 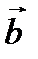 коллинеарны.
коллинеарны.
Пусть векторы 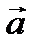 и
и 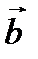 даны своими координатами:
даны своими координатами: 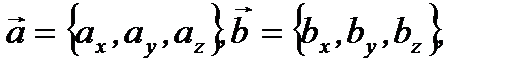 то есть
то есть
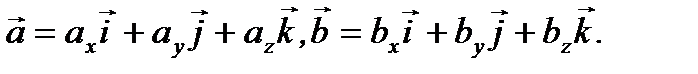 (2.19)
(2.19)
Вычислим векторное произведение 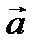 и
и 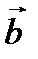 с учетом (2.19). Имеем
с учетом (2.19). Имеем
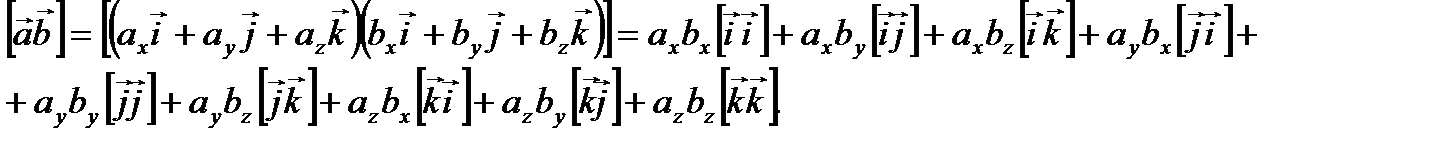 (2.20)
(2.20)
Учитывая, что
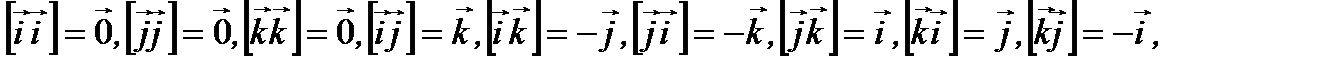 (2.21)
(2.21)
из (2.20) получим
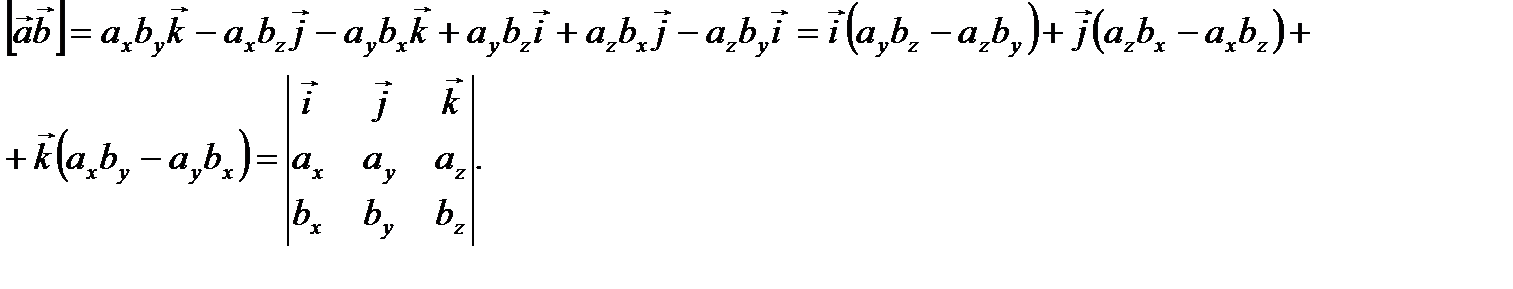 (2.22)
(2.22)
(2.22) представляет выражение векторного произведения двух векторов 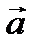 и
и 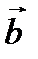 в координатах.
в координатах.
Если векторы 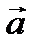 и
и 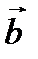 коллиенарны, то
коллиенарны, то 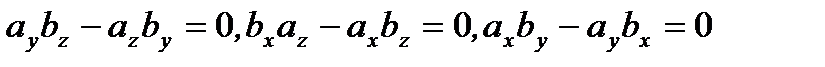 , то есть
, то есть
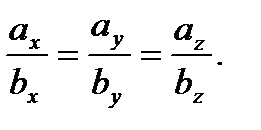 (2.23)
(2.23)
Условие (2.23) означает, что если векторы 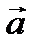 и
и 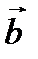 коллинеарны, то их соответствующие координаты пропорциональны.
коллинеарны, то их соответствующие координаты пропорциональны.
Пример 2.9. Даны координаты вершин треугольника в трехмерной прямоугольной системе координат: 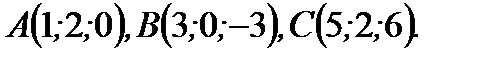 Определить площадь
Определить площадь 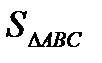 этого треугольника (рис. 2.10).
этого треугольника (рис. 2.10).
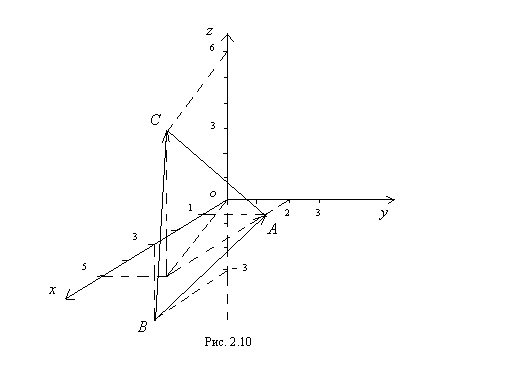
Решение.Заметим, что векторы 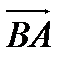 и
и 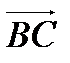 имеют координаты:
имеют координаты:
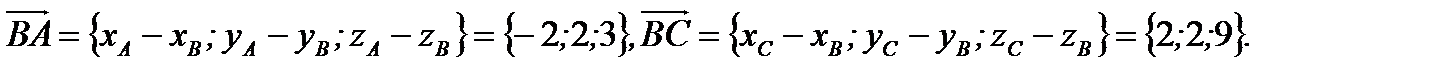
По определению модуля векторного произведения двух векторов имеем
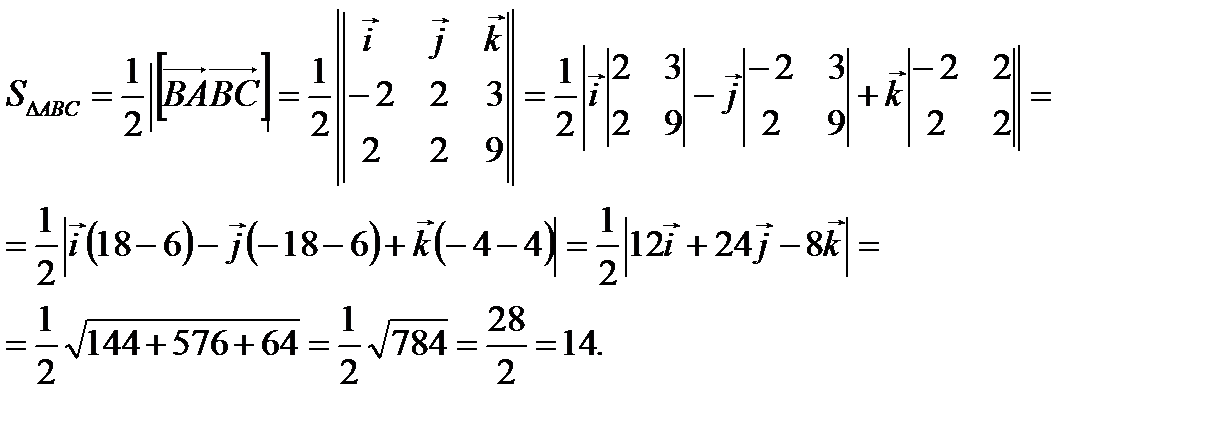 Ответ: 14.
Ответ: 14.
Дата добавления: 2018-11-25; просмотров: 675;
