Скалярное произведение двух векторов.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов умноженное на косинус угла между ними, то есть
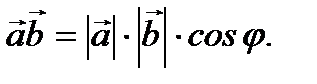 (2.13)
(2.13)
Так как 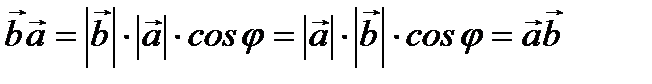 , то
, то 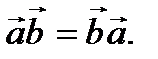 Это означает, что если в скалярном произведении поменять векторы местами, то его значение не изменится.
Это означает, что если в скалярном произведении поменять векторы местами, то его значение не изменится.
Если векторы 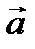 и
и 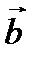 даны своими координатами в двумерной системе координат, то есть
даны своими координатами в двумерной системе координат, то есть 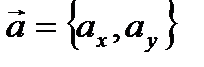 и
и 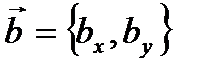 , то их скалярное произведение равно
, то их скалярное произведение равно
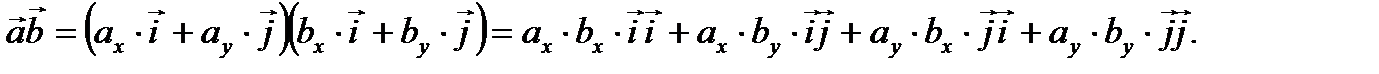 (2.14)
(2.14)
Используя то, что
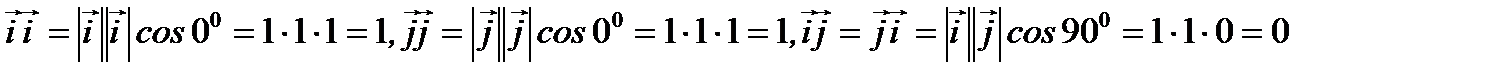 ,
,
из (2.14) получим
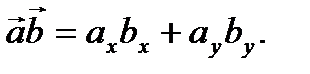 (2.15)
(2.15)
Аналогичный результат получается и в случае, когда векторы 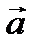 и
и 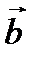 со своими координатами даны в трехмерной прямоугольной системе координат. Итак
со своими координатами даны в трехмерной прямоугольной системе координат. Итак
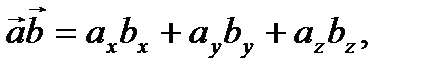 (2.16)
(2.16)
где 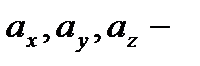 координаты вектора
координаты вектора 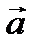 , а
, а 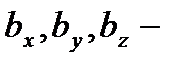 координаты вектора
координаты вектора 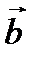 . (2.15) и (2.16) представляют выражения скалярного произведения двух векторов в координатах.
. (2.15) и (2.16) представляют выражения скалярного произведения двух векторов в координатах.
Из (2.13) с учетом (2.16) нетрудно заметить, что
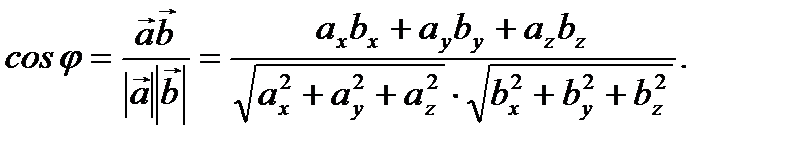 (2.17)
(2.17)
Теорема 2.1.Равенство нулю скалярного произведения двух не нулевых векторов 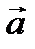 и
и 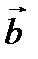
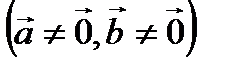 является необходимым и достаточным условием перпендикулярности векторов
является необходимым и достаточным условием перпендикулярности векторов 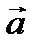 и
и 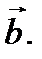
Доказательство:
Необходимость. Дано, что 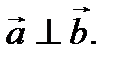 Доказать, что
Доказать, что 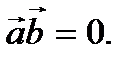
На самом деле, по условию теоремы векторы перпендикулярны, значит угол 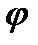 между ними равен
между ними равен 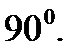 Тогда
Тогда 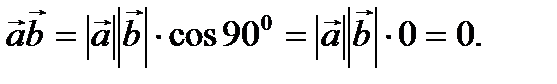
Достаточность. Дано, что 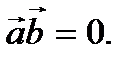 Доказать, что
Доказать, что 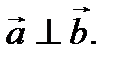 По условию теоремы и с учетом
По условию теоремы и с учетом
(2.13) имеем 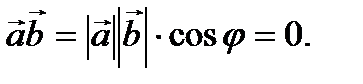 Но так как ни один из векторов не нулевой, то
Но так как ни один из векторов не нулевой, то 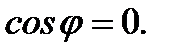
Отсюда следует, что 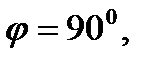 то есть
то есть 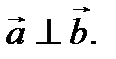
Пример 2.5. Даны векторы 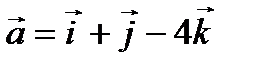 и
и  Найти угол
Найти угол 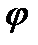 между ними.
между ними.
Решение.Очевидно, что 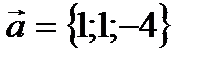 и
и 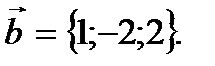 Тогда по формуле (2.17) имеем
Тогда по формуле (2.17) имеем
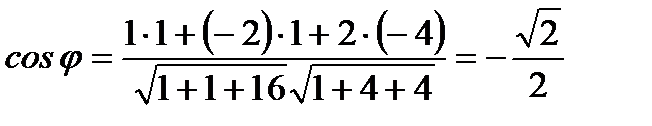 и
и 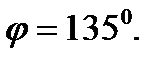
Ответ: 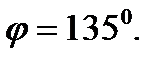
Пример 2.6. Показать, что векторы 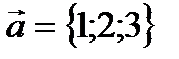 и
и 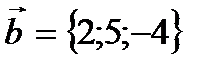 перпендикулярны.
перпендикулярны.
Решение.Скалярное произведение этих векторов, вычисленное по формуле (2.16), равно
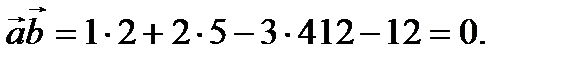 Тогда согласно теореме 2.1 векторы
Тогда согласно теореме 2.1 векторы 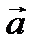 и
и 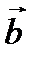 перпендикулярны.
перпендикулярны.
Ответ: 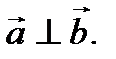
Пример 2.7. Найти проекцию вектора 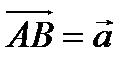 на ось
на ось 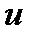 (рис. 2.7).
(рис. 2.7).
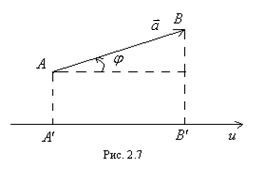
Решение.Согласно рисунку 2.7 имеем
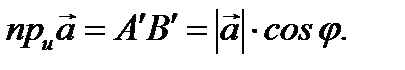
Ответ: 
Пример 2.8. Даны векторы 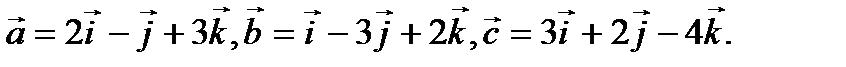 Найти вектор
Найти вектор  который удовлетворяет условиям
который удовлетворяет условиям 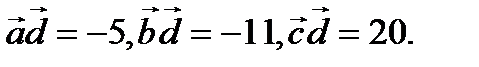
Решение.Согласно (2.16) имеем
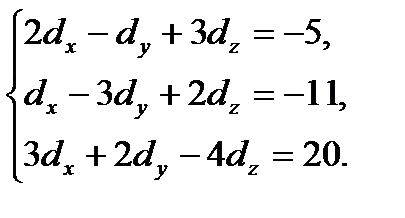
Решение полученной системы найдем по правилам Крамера (2.10), предварительно вычисляя определители 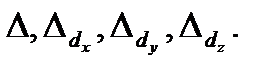
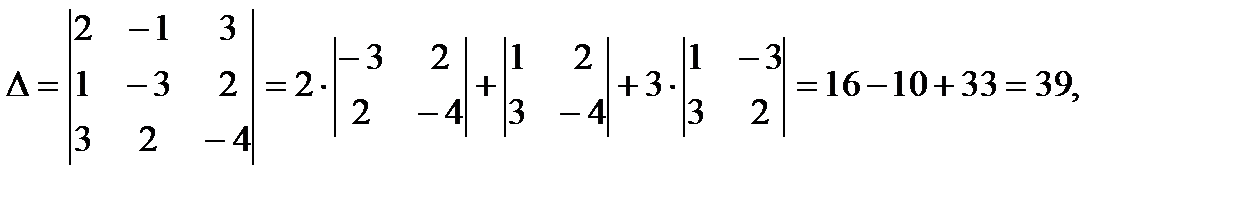
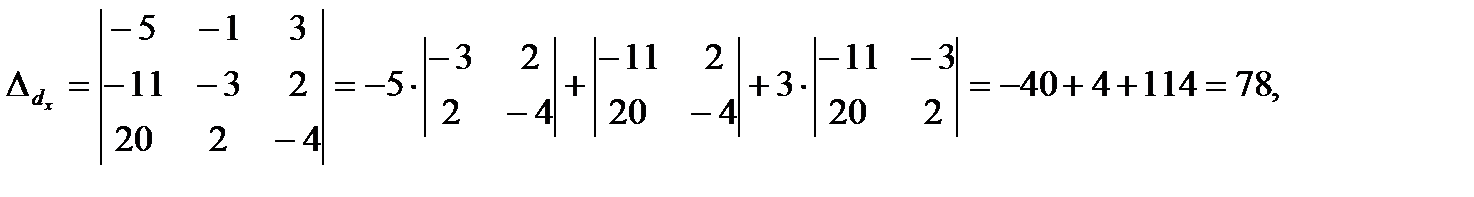
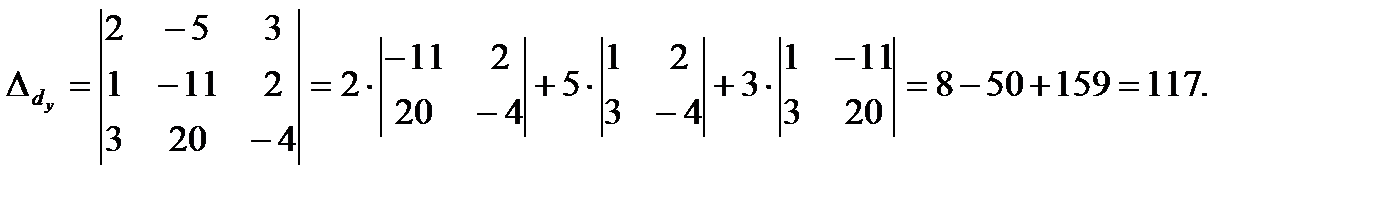
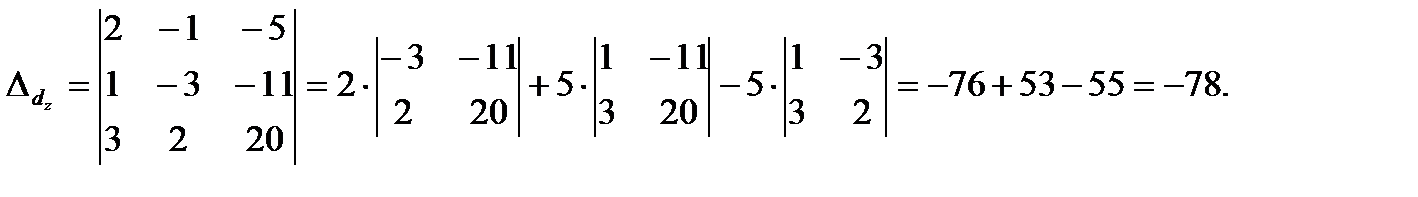
Тогда по формулам (2.10) найдем координаты вектора 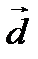 в виде
в виде
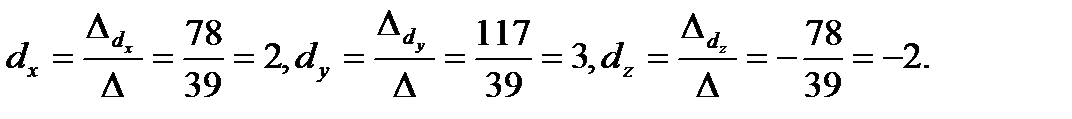
Таким образом, получаем, что 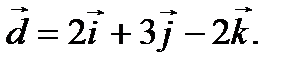
Ответ: 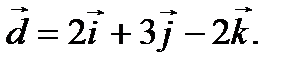

Дата добавления: 2018-11-25; просмотров: 623;
