Декартово произведение множеств
Декартово, или прямое, произведение множеств введено в 1637г. французским математиком Р. Декартом (1596–1650 гг.).
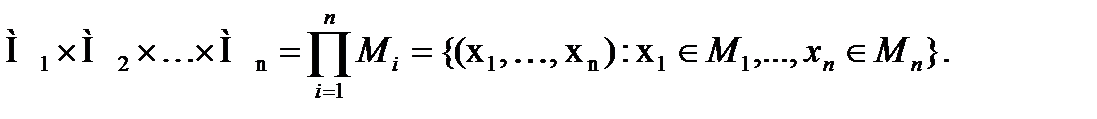 Элементами этого произведения–множества являютсянаборы, или кортежи. Набор длины n – это последовательность n элементов, например (x1, x2, …, xn). Здесь, в отличие от множества, порядокважен.
Элементами этого произведения–множества являютсянаборы, или кортежи. Набор длины n – это последовательность n элементов, например (x1, x2, …, xn). Здесь, в отличие от множества, порядокважен.
Итак,
Если все множества одинаковы, получается декартова степень:
М  М
М  …
…  М = Мn.
М = Мn.
n
Декартово произведение некоммутативно: X  Y ¹ Y
Y ¹ Y  X.
X.
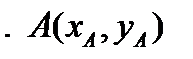 Примеры:
Примеры:
R
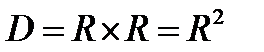
R
шахматная доска: W={a,b,…,h}, G={1,2,…,8}, D = W×G = {(a,1)…(h,8)}, |D|=64
Декартовым (прямым) произведением A ´ B множеств A и B является множество всех упорядоченных пар (x, y), где x Î X и y Î Y:
A ´ B=í(x, y): xÎA & yÎBý.
Пример: А={-1;0;2}, В={3;6}
Ах В={(-1;3), (-1;6), (0;3), (0;6), (2;3), (2;6)}.
Пример: А=[-1;4), В=R
| -1 |
| х |
| у |
| А*В |
Нарисовать декартово произведение окружности с отрезком, длиной [0,1]
Свойства декартова произведения
1° АхВ¹ВхА
2° Если у нас имеются 3 непустых множества А, В, С и множество АÍВ, тогда декартово произведение АхСÍВхС
3° Если даны любые три непустые множества А, В, С и АхВÍВхСÞ АÍС
4° Пусть нам даны любые три непустые множества А, В, С, тогда
Ах(В  С)=(АхВ)
С)=(АхВ)  (АхС)
(АхС)
G F
При доказательстве будем использовать антисимметричность отношения включения.
Доказательство разобьется на 2 этапа:
1) GÍF
Þ F=G
2) FÍG
1. Покажем, что GÍF, для этого зафиксируем пару (х,у)ÎG или (х,у)ÎАх(В  С)
С)
хÎА и уÎ(В  С) Þ хÎА и уÎВ или уÎС Þ (х,у)Î АхВ или (х,у)Î АхС Þ
С) Þ хÎА и уÎВ или уÎС Þ (х,у)Î АхВ или (х,у)Î АхС Þ
Þ (х,у)Î(АхВ)  (АхС) Þ GÍF
(АхС) Þ GÍF
2. Покажем, что FÍG (доказать самостоятельно)
Из (1) и (2) Þ G=F
Утверждение: Пусть nÎN. Множество А1, А2,…, Аn непустые. Пусть множество Аi – конечное, тогда |А1хА2х…хАn|=|А1|×|А2|×…×|Аn| (*)
Для доказательства будем использовать метод математической индукции. База индукции: n=2. Рассмотрим два множества с мощностями |А1|=n и |А2|=m.
1) Пусть А1={а1, а2,…, аn}, множество А2={ b1,b2,…, bm}. Выполним декартово произведение множеств.
А1х А2={(а1,b1), (а1,b2),…,(а1,bm),(а2,b1), (а2,b2),…,(а2,bm),…,(аn,b1), (аn,b2),…,(аn,bm)}
|А1хА2|=nхm=|А1|×|А2|.
2) Предположим, что наша функция (*) верна для всех k=n-1, т.е.
|А1хА2х…хАn-1|=|А1|× |А2|×…×|Аn-1| (**)
3) Осуществляем индукционный переход, рассмотрим мощность декартова произведения n множеств, по пункту (1).
Можно записать |А1хА2х…хАn|=|А1|×|В|, где В=А2х…хАn, т.е. формула (**) может быть использована
|А1хА2х…хАn|=|А1|×|В|=|А1|×|А2|×…×|Аn|
Из (1-3) следует, что наша формула (*) верна для всех nÎN/{1}.
Дата добавления: 2017-08-01; просмотров: 1214;
