Полиномиальная теорема

(а₁+а₂+…+а_k)ⁿ=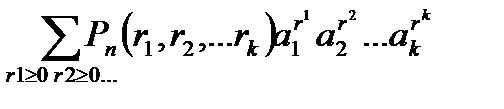

Перемножим сумму k слагаемых на себя n раз

(а₁+а₂+…+а_k)… (а₁+а₂+…+а_k), получим kⁿ слагаемых вида d₁d₂…d_n, где каждый множитель d_i равен либо а₁,а_2,…,а_k. Обозначим В(r₁, r₂, …,r_k) совокупность всех тех слагаемых, в которых элемент а₁ встречается r₁ раз, а₂ встречается r₂ раза, а_k встречается r_k раз. Число таких слагаемых равно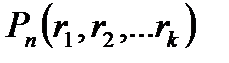

Пусть элемент а повторяется r раз, элемент b – (n-r) раз соответственно, полиномиальный коэффициент

Р_n(r,n-r)=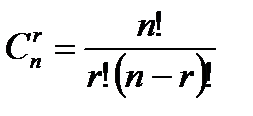

Упражнение: Покажите, что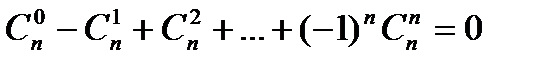

Отношения. Основные понятия

Отношения – это один из способов задания взаимосвязей между элементами множества. Наиболее распространены унарные и бинарные отношения.

Унарные (одноместные) отношения отражают наличие какого-либо определенного признака R у элементов множества A.

Все элементы множества A, обладающие признаком R, образуют некоторое подмножество: A^R = ía: aÎA & aÎRý.

Бинарные (двухместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множества A. Например, на множестве людей могут быть заданы следующие бинарные отношения: «жить в одном городе», «учиться в одном институте».

В общем случае отношения могут быть n-местными. Под n-местным отношением понимают подмножество R прямого произведения n множеств:

RÍM₁´M₂´¼´M_n.

Бинарным отношением R называется подмножество пар (a,b) Î R декартового произведения M₁´M₂, где R Í M₁´M₂. Множество M₁ – область определения отношения R, множество M₂ – область значений отношения R.

Если задано отношение R между парами элементов одного и того же множества M, то R Í M´M.

Вместо записи (a,b) Î R используют также обозначение a R b.

Шахматная доска доставляет пример бинарного отношения на множестве горизонталей G = {1, 2, …, 8} и множестве вертикалей W = {a, b, …, h}. В результате получается множество клеток доски: D = W * G = {(a, 1), (a, 2), …, (h, 8)}, |D| =64.

Выделяются три отношения:

– пустое отношение, Æ Í М²;

– универсальное отношение, U_M = {(x, y): x, y Î M};

– тождественное отношение, I_M = {(x, x): x ÎM}.

Область D(R) определения и область значений Q(R) отношения R определяются в виде:

D(R) = ía: (a,b)ÎRý, Q(R) = íb: (a,b)ÎRý.

Задать бинарные отношения можно любым способом задания множеств:

1) В виде характеристического свойства R = í(a,b): (a,b)ÎRý, где в правой части равенства вместо R записывается характеристическое свойство.

2) Списком (перечислением) пар, для которых выполняется данное отношение. Например, R = í(a,b), (a,d), (b,c)ý.

3) Матрицей. Отношению R Í M´M, где M = ía₁, a₂, ¼, a_ný, соответствует квадратная матрица порядка n, в которой элемент c_ij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между a_i и a_j имеет место отношение R, или 0, если оно отсутствует:

.

Пример 2.1. Пусть M = í1, 2, 3, 4, 5ý. Задать в виде характеристического свойства, списком (в явном виде) и матрицей отношение R Í M´M, если R означает «быть меньше».

Решение. Отношение R как множество содержит все пары элементов a,b из M, такие что a<b. Тогда отношение R в виде характеристического свойства имеет вид:

R = í(a,b): a<b, a,bÎMý.

В виде списка отношение R выглядит следующим образом:

R = í(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5)ý.

Матрица отношения R приведена на рис. 2.2.

Можно рассмотреть несколько вариантов графического представления отношений:

– точки в плоскости D F;

– ориентированные отрезки (со стрелками)

от точек оси абсцисс, соответствующих левым

элементам пар, к точкам оси ординат,

соответствующих правым элементам;

– двудольный орграф

(левая доля соответствует области определения

D, правая – области значений F);

– ориентированный граф порядка, равного мощности бинарного отношения (рис. 7).

М = {1, 2, 3, 4}, R = {(1, 2), (1, 4), (2, 3), (2, 4), (3, 4), (4, 1)} (рис. 7а).

Рис. 7. Графическое представление отношений

На рис. 7б и 7в представлены также графы тождественного отношения I_М и универсального отношения U_М.

Свойства отношений

Основнымисвойствами отношений являются:

– рефлексивность; – симметричность; – транзитивность; – антисимметричность;

Рефлексивность означает: справедливо xrx для любогоx Î M.

В графе отношения все вершиныимеют петли. (например, отношение «жить в одном городе» – рефлексивно);

R – антирефлексивно, если ни для какого a Î M имеет место a R a (например, отношение «быть сыном» – антирефлексивно);

Симметричность:xry Þ yrx. (например, отношение «учиться в одном институте» – симметрично)

При этом может быть и «пустая» симметричность когда нет xry («на нет и суда нет»). В графе соответствия каждая дуга имеет пару, но может быть и отсутствие связи между двумя вершинами.

Транзитивность:xry и yrz Þ xrz. «быть моложе» – транзитивно

Для каждой пары связанных непрямовершин существует и прямая связь (замыкающая образующийся многоугольник в графе отношения).

Транзитивность может быть и вырожденная (пустая, когда условие в левой части (до двойной стрелки) не выполняется). Здесь опять «на нет и суда нет».

Антисимметричность:xry и yrx Þ x = y. т.е. ни для каких различных элементов a, b (a ¹ b) не выполняется одновременно a R b и b R a (например, отношения «быть сыном», «быть начальником» – антисимметричны);

В графе отношений нет ни однойдвойной связи. И антисимметричность может быть пустой – вообще нет никакой прямой связи между двумя вершинами. Таким образом, в графе отношений допускаются только одинарные прямые связи.

асимметричность,… означает: прямые связи есть и двойные, и одинарные, и «никакие», т.е. нет ни симметричности, ни антисимметричности.

Свойства симметричности и антисимметричности не являются взаимно исключающими. Они могут “сосуществовать”. Правда, это возможно только в пустом варианте (рис. 8.)

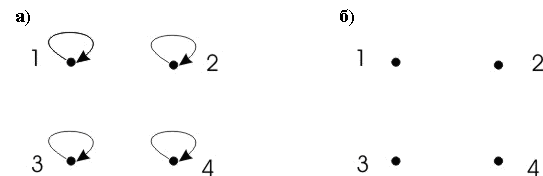
Рис. 8. Примеры одновременных симметричности и антисимметричности

Отмеченные выше свойства отношений являются относительно редкими. Например, отношение, представленное графом на рис. 9, не является ни рефлексивным (P), ни симметричным (C), ни транзитивным (T) и ни антисимметричным (А).

Рис. 9. Пример отношения.

Наконец, отметим ошибочность утверждения о том, что из симметричности и транзитивности якобы вытекает рефлексивность, т.е. что последнее свойство является производным от первых двух и петли в графе отношения появляются сами собой:

С: xry Þ yrx, А: xry и yrz Þ xrz;

при x = z получается как будто рефлексивность:

Р: xrx.

На самом деле это, конечно, не так. Убедиться в этом (доказать это) предоставляется читателю. (На примере?)

Пример: А={1,2,3}

r₁={(1,1), (3,3), (1,2)} нерефлексивно, несимметрично, транзитивно

r₂={(1,1), (3,3), (2,2)} рефлексивно, симметрично, транзитивно, эквивалентно на А, антисимметрично

r₃={(1,2), (2,1)} антирефлексивно, симметрично, нетранзитивно

r₄={(1,1), (3,3), (1,2), (2,1)} нерефлексивно, симметрично, нетранзитивно

r₅={(1,1)} нерефлексивно, симметрично, транзитивно

r₆={(1,2)} антирефлексивно, несимметрично, транзитивно

r₇=r₂È{(1,3), (3,1)} эквивалентно

r₈=r₂È{(1,3), (3,1), (2,3)} рефлексивно, несимметрично, нетранзитивно

Пусть задано некоторое множество А, разбиение будем называть U.

Определение: Совокупность подмножеств множества А будем называть разбиением данного множества, если:

1) А_iÇA_j=Æ, i¹j

2) .

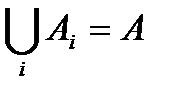Пример: Дано множество В=R=(-¥;1)È[1;2] È[2;¥)

А₁ А₂ А₃

Является ли разбиением данные подмножества?

U={А₁,А₂,А₃} - не является

Пусть задано множество В={-1;4;7}

U₁={-1,{4,7}} не является разбиением

U₂={{-1,4,7}} является разбиением

U₃={{-1},{4},{7}} является разбиением

U₄={{-1,4},{7}} является разбиением

U₅={{-1,4},{4,7}} не является разбиением