Независимость событий. Теорема умножения вероятностей
Из определения условной вероятности следует, что
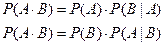 . .
| (3.5) |
т.е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
Равенство (3.5) называют правилом или теоремой умножения вероятностей. Это правило обобщается на случай n событий.
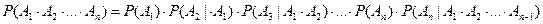 . .
| (3.6) |
Для трех событий А1, А2, А3 получаем:
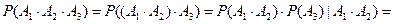
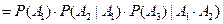 .
.
Правило умножения вероятностей имеет простой вид, если события, образующие произведение, независимы.
Событие А называется независимымот события В,если его условная вероятность равна безусловной, т.е. если выполняется равенство
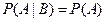 . .
| (3.7) |
Лемма 3.1 (о взаимной независимости событий).Если событие А не зависит от события В, то и событие В не зависит от события А.
Доказательство. Из равенства (3.5), с учетом равенства (3.7), следует
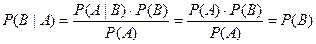 , т.е. , т.е. 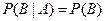 , ,
| (3.8) |
а это означает, что событие В не зависит от события А.
Можно дать следующее определение независимости событий.
Два, события называются независимыми, если появление одного из них не меняет вероятность появления другого.
Для независимых событий правило умножения вероятностей принимает вид:
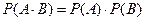 , ,
| (3.9) |
т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Равенство (3.9) часто используют в качестве определения независимости событий: события А и В называются независимыми, если 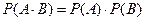 .
.
Можно показать, что если события А и В независимы, то независимы события 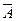 и В, А и
и В, А и 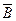 ,
, 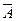 и
и 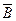 .
.
На практике о независимости тех или иных событий часто судят исходя из интуитивных соображений и анализа условий опыта, считая независимыми события, «между которыми нет причинно-следственных связей».
Понятие независимости может быть распространено на случай n событий.
События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае события А1,А2,…,Аn называются зависимыми.
Для независимых событий их условные вероятности равны безусловным и формула (3.6) упрощается:
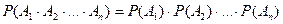 . .
| (3.10) |
Из попарной независимости событий А1,А2,…,Аn (любые два из них независимы) не следует их независимость в совокупности (обратное верно).
Пример 3.3. Производится выбор флага из 4-х, имеющихся в наличии: красного, голубого, белого и трехцветного (красно-бело-голубого). Исследовать на независимость события: К – выбранный флаг имеет красный цвет, Г –голубой цвет, Б – белый.
Решение:
Возможных исходов выбора 4. Событию К благоприятствуют 2 исхода, т.к. красный имеется у двух флагов. Поэтому 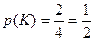 . Аналогично находим, что
. Аналогично находим, что 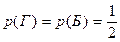 . Событию К∙Г – выбран флаг, имеющий 2 цвета (красный и голубой), - благоприятствует один исход. Поэтому,
. Событию К∙Г – выбран флаг, имеющий 2 цвета (красный и голубой), - благоприятствует один исход. Поэтому, 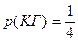 . И так как
. И так как 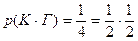 , т.е.
, т.е. 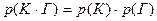 , то события К и Г независимы. Аналогично убеждаемся в независимости событий К и Б, Б и Г. Значит, события К, Б, Г попарно независимы. Но
, то события К и Г независимы. Аналогично убеждаемся в независимости событий К и Б, Б и Г. Значит, события К, Б, Г попарно независимы. Но 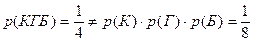 , следовательно события К, Г и Б не являются независимыми в совокупности.
, следовательно события К, Г и Б не являются независимыми в совокупности.
Дата добавления: 2017-03-29; просмотров: 411;
