Формула полной вероятности
Одним из следствий совместного применения теорем сложения и умножения вероятностей являются формулы полной вероятности и Байеса. Напомним, что события А1,А2,…..,Аn образуют полную группу, если 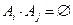 ,
, 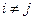 и
и 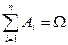 . Систему таких событий называют также разбиением.
. Систему таких событий называют также разбиением.
Теорема 3.2.Пусть события 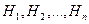 образуют полную группу. Тогда для любого события А имеет место формула полной вероятности или средней вероятности.
образуют полную группу. Тогда для любого события А имеет место формула полной вероятности или средней вероятности.
 . .
| (3.11) |
Доказательство. Так как 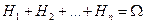 , то в силу свойств операций над событиями,
, то в силу свойств операций над событиями, 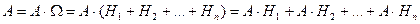 . Из того, что
. Из того, что 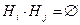 , следует, что
, следует, что 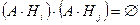 ,
, 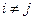 , т.е. события
, т.е. события 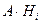 и
и 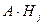 также несовместны. Тогда по теореме сложения вероятностей
также несовместны. Тогда по теореме сложения вероятностей
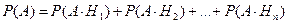 , т.е.
, т.е. 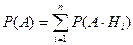 .
.
По теореме умножения вероятностей 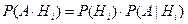 , откуда и следует формула (3.11).
, откуда и следует формула (3.11).
Отметим, что в формуле (3.11) события 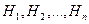 обычно называют гипотезами; они исчерпывают все возможные предположения (гипотезы) относительно исходов как бы первого этапа опыта, событие А - один из возможных исходов второго этапа.
обычно называют гипотезами; они исчерпывают все возможные предположения (гипотезы) относительно исходов как бы первого этапа опыта, событие А - один из возможных исходов второго этапа.
Пример 3.4.В сборочный цех завода поступает 40% деталей из I цеха и 60% - из II цеха. В I цехе производится 90% стандартных деталей, а во II – 95%. Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной.
Решение:
Взятие детали можно разбить на два этапа.
Первый этап – это выбор цеха. Имеется две гипотезы: Н1 – деталь изготовлена I цехом, Н2 – II цехом.
Второй этап – взятие детали. Событие А – взятая на удачу стандартная деталь. Очевидно, события Н1 и Н2 образуют полную группу, Р(Н1)=0,4, Р(Н2)=0,6.
Числа 0,90 и 0,95 являются условными вероятностями события А при условии гипотез Н1 и Н2 соответственно, т.е.
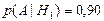 и
и 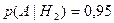 .
.
По формуле (3.11) находим
 .
.
Формула Байеса
Следствием формулы (3.11) является формула Байеса или теорема гипотез. Она позволяет переоценить вероятности гипотез Нi, принятых до опыта и называемых априорными по результатам уже проведенного опыта, которые называются апостериорными,т.е. найти условные вероятности 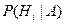 .
.
Теорема 3.3Пусть события 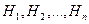 образуют полную группу событий. Тогда условная вероятность события Hk
образуют полную группу событий. Тогда условная вероятность события Hk 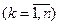 при условии, что событие А произошло, задается формулой:
при условии, что событие А произошло, задается формулой:
 . .
| (3.12) |
где 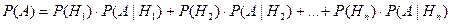 – формула полной вероятности. Формула (3.12) называется формулой Байеса.
– формула полной вероятности. Формула (3.12) называется формулой Байеса.
Доказательство. Применив формулы условной вероятности и умножения вероятностей, имеем
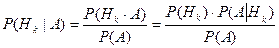 ,
,
где Р(А) – формула полной вероятности.
Пример 3.5. В примере 3.4. найти вероятность того, что эта стандартная деталь изготовлена II цехом.
Решение:
Определим вероятность гипотезы H2 при условии, что событие А (взятая стандартная деталь) уже произошло, т.е. 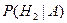 :
:
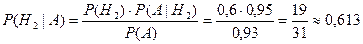 .
.
Дата добавления: 2017-03-29; просмотров: 250;
