Теорема сложения вероятностей
Вероятность суммы двух несовместных событий определяется аксиомой А3:
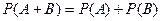 ,
, 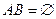 .
.
Выведем формулу вероятностей двух совместных событий.
Теорема 3.1. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения
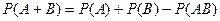 . .
| (3.1) |
Доказательство. Представим события 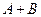 и В в виде суммы двух несовместных событий:
и В в виде суммы двух несовместных событий: 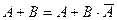 ,
, 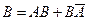 . В справедливости формул можно наглядно убедиться на рис.1.
. В справедливости формул можно наглядно убедиться на рис.1.
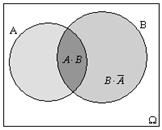
Рис. 1
Тогда согласно аксиоме А3, имеем: 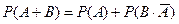 и
и 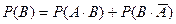 . Отсюда следует
. Отсюда следует 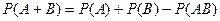 .
.
Формула (3.1) справедлива для любых событий А и В.
Можно получить формулу вероятности суммы трех и большего числа совместных событий. Для трех событий она имеет вид:
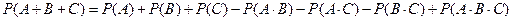 . .
| (3.2) |
Вероятность суммы нескольких совместных событий 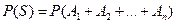 , можно найти, используя равенство
, можно найти, используя равенство 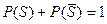 , где
, где 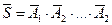 - противоположно событию S. Тогда
- противоположно событию S. Тогда 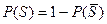 .
.
Пример 3.1. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?
Решение:
Введем события: А – появление шестерки на первой кости, В – появление шестерки на второй кости. Тогда А+В – появление хотя бы одной шестерки при бросании костей. События А и В совместные. По формуле (3.1) находим
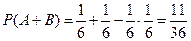 .
.
Иначе: 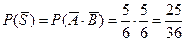 . Следовательно,
. Следовательно, 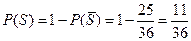 .
.
Дата добавления: 2017-03-29; просмотров: 228;
