Условные вероятности
Пусть А и В – два события, рассматриваемые в данном опыте. Наступление одного события может влиять на возможность наступление другого. Для характеристики зависимости одних событий от других вводится понятие условной вероятности.
Условной вероятностью события В при условии, что произошло событие А, называется отношение вероятности произведения этих событий к вероятности события А, причем 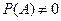 , обозначается символом
, обозначается символом 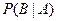 . Таким образом, по определению:
. Таким образом, по определению:
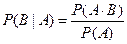 , , 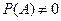 . .
| (3.3) |
Вероятность Р(В), в отличии от условной, называется безусловной вероятностью.
Аналогично определяется условная вероятность события А при условии В, т.е. 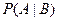 :
:
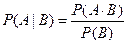 , , 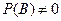 . .
| (3.4) |
Отметим, что условная вероятность, скажем 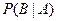 , удовлетворяет аксиомам Колмогорова:
, удовлетворяет аксиомам Колмогорова:
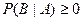 ,
,
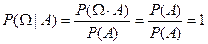 ,
,
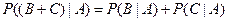 , если
, если 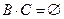 .
.
Поэтому для условной вероятности справедливы все свойства из аксиом.
Пример 3.2. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают два шара. Какова вероятность того, что 2-й шар окажется белым при условии, что 1-й шар был черным?
Решение:
1-й способ. Пусть А – 1-й шар черный, В – 2-й шар белый. Так как событие А произошло, то в урне осталось 8 шаров, из которых 2 белых. Поэтому 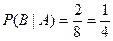 .
.
2-й способ. Найдем 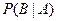 по формуле (3.3). очевидно, что
по формуле (3.3). очевидно, что 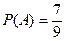 . Находим
. Находим 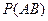 :
: 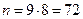 - общее число исходов (появление двух шаров). Событию АВ благоприятствуют
- общее число исходов (появление двух шаров). Событию АВ благоприятствуют 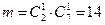 исходов. Поэтому
исходов. Поэтому 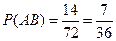 . Следовательно,
. Следовательно,
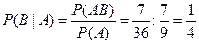 .
.
Дата добавления: 2017-03-29; просмотров: 233;
