Классическое определение вероятности
Если множество элементарных событий 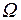 состоит из n равновозможных элементарных событий, то вероятность р(А) события А равна числу m элементарных событий, входящих в А, деленному на число всех элементарных событий, т. е.
состоит из n равновозможных элементарных событий, то вероятность р(А) события А равна числу m элементарных событий, входящих в А, деленному на число всех элементарных событий, т. е. 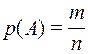 .
.
Условной вероятностью 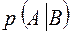 называют вероятность события А, вычисленную в предположении, что событие В уже наступило.
называют вероятность события А, вычисленную в предположении, что событие В уже наступило.
Условная вероятность 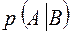 события А при условии, что событие В произошло, определяется формулой
события А при условии, что событие В произошло, определяется формулой
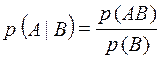 , где
, где 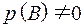 .
.
События А и В – называются независимыми, если при происхождении одного из них не изменяется вероятность происхождения другого. Для независимых событий выполняется равенство 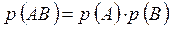 .
.
Очевидно, что для независимых событий справедливо:
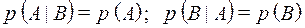 .
.
События 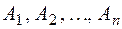 называются независимыми в совокупности, если для любых k из них
называются независимыми в совокупности, если для любых k из них 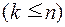 выполняется соотношение:
выполняется соотношение:
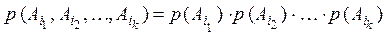 .
.
Если это соотношение выполняется при k = 2, то события 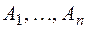 называются попарно независимыми.
называются попарно независимыми.
Теорема сложения.
Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
p(А+В) = p(А) + p(В) – p(АВ).
Если события А и В несовместны, то p(А+В) = p(А) + p(В).
Теорема умножения.
Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило:
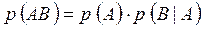 .
.
Если события А и В независимы, то 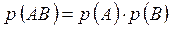 .
.
Пример 1. Брошены три монеты. Найти вероятность того, что выпадут две “решки”.
Пространство элементарных событий данного стохастического эксперимента: 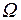 = {ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР} состоит из 8 равновозможных исходов (
= {ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР} состоит из 8 равновозможных исходов ( 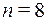 ). Число благоприятных элементарных исходов для события A = «выпали две “решки”» = {ОРР, РОР, РРО} равно 3 (
). Число благоприятных элементарных исходов для события A = «выпали две “решки”» = {ОРР, РОР, РРО} равно 3 ( 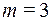 ). Следовательно,
). Следовательно, 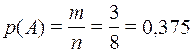 .
.
Пример 2. В студенческой группе из 15 девушек и 10 юношей по жребию разыгрывается билет в театр. Какова вероятность, что билет достанется девушке? Событию A = «билет достался девушке» благоприятствует 15 элементарных событий ( 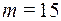 ) из 25 равновозможных (
) из 25 равновозможных ( 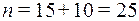 ).
).
Следовательно, 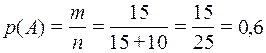 .
.
Пример 3. Студент пришел на экзамен, зная лишь 20 из 25 вопросов программы. Экзаменатор задал студенту 3 вопроса. Найти вероятность того, что студент знает все эти вопросы.
Рассмотрим событие А = «студент знает ответы на все три заданных вопроса». Оно состоит из события 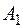 – «студент знает ответ на 1-ый вопрос» Исобытия
– «студент знает ответ на 1-ый вопрос» Исобытия 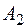 – «студент знает ответ на 2-ой вопрос» И события
– «студент знает ответ на 2-ой вопрос» И события 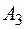 – «студент знает ответ на 3-ий вопрос».
– «студент знает ответ на 3-ий вопрос». 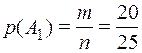 . Если студент ответил на первый вопрос, то всего осталось 19 вопросов, которые он знает из 24 оставшихся, следовательно, вероятность второго события, при условии, что первое произошло равна
. Если студент ответил на первый вопрос, то всего осталось 19 вопросов, которые он знает из 24 оставшихся, следовательно, вероятность второго события, при условии, что первое произошло равна 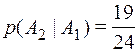 . Аналогично
. Аналогично 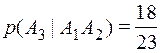 .
.
Таким образом, по теореме умножения вероятностей
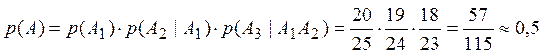 .
.
(Или по классическому определению вероятности: 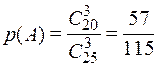 , где число благоприятных событий
, где число благоприятных событий 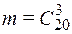 число – сочетаний из 20 знакомых вопросов по три; число всевозможных событий
число – сочетаний из 20 знакомых вопросов по три; число всевозможных событий 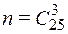 – число сочетаний из всех 25 вопросов по три.)
– число сочетаний из всех 25 вопросов по три.)
Пример 4. Для сигнализации о возгорании установлены два независимо работающих датчика. Вероятности того, что при возгорании датчик сработает для первого и второго датчиков соответственно равны 0,9 и 0,95. Найти вероятность того, что при пожаре сработает: а) хотя бы один датчик; б) только один датчик.
Обозначим: 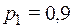 – вероятность срабатывания 1-го датчика, тогда вероятность его несрабатывания равна
– вероятность срабатывания 1-го датчика, тогда вероятность его несрабатывания равна 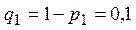 ;
; 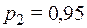 – вероятность срабатывания 2-го датчика, тогда вероятность его несрабатывания равна
– вероятность срабатывания 2-го датчика, тогда вероятность его несрабатывания равна 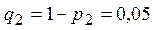 .
.
Вероятность того, что при возгорании сработает хотя бы один датчик (событие А) можно вычислить по теореме сложения вероятностей: 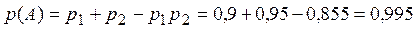 или через противоположное событие (оба датчика не сработали):
или через противоположное событие (оба датчика не сработали): 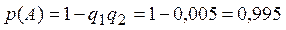 .
.
Вероятность того, что при возгорании сработает только один датчик (событие В) равна 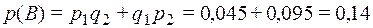 .
.
Дата добавления: 2018-09-24; просмотров: 553;
