Соответствия и функции

Соответствием множеств А и В называется подмножество G такое, что 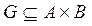. Если 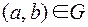, то говорят, что “b соответствует a при соответствии G”. Область определения соответствия G – множество пр₁ G Í A. Область значений соответствия G – множество пр₂G Í B.

Соответствие G называетсявсюду (полностью) определенным– если пр₁ G = А (в противном случае – частично определенное соответствие). Соответствие G называетсясюрьективным, если пр₂ G = B.

Образэлемента aв множестве B при соответствии G – это множество всех элементов 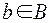, которые соответствуют 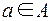. Прообразэлемента b в множестве А при соответствии G – это множество всех 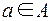, которым соответствует .

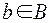Образом множестваСÎ пр₁ G называется объединение образов всех элементов С. Прообразом множестваD Î пр₂ G называется объединение прообразов всех элементов D.

Соответствие G называетсяфункциональным (однозначным)соответствием, если образом любого элемента из пр₁ G является единственный элемент из пр₂ G.

Соответствие G называетсяинъективнымсоответствием, если прообразом любого элемента из пр₂ G является единственный элемент из пр₁ G.

Соответствие F является функцией типа 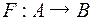, если оно функционально (однозначно) ( ).

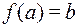Соответствие G является отображением множества А в множество В, если оно функционально и полностью определено.

Соответствие G является взаимно однозначным, если оно: 1) всюду определено; 2) сюрьективно; 3) функционально; 4) инъективно.

Преобразованием множестваАназывается отображение типа .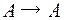

Функция типа 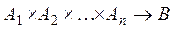называется n-местной функцией ( ).

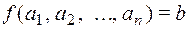Соответствие 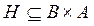называется обратным к 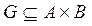, если Н таково, что .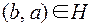

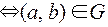Если соответствие, обратное к функции 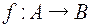является функциональным, то оно называется функцией, обратной к f ( ).

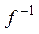Пусть дана функция 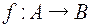. Соответствие 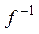является функцией тогда и только тогда, когда f инъективна, и 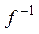является отображением тогда и только тогда, когда f инъективна и сюрьективна (т.е. биективна).

Утверждение:Для функции 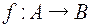существует обратная функция 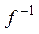тогда и только тогда, когда f является взаимнооднозначным соответствием между своей областью определения и областью значений.

Пусть даны функции 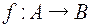и .

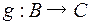Функция 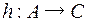называется композицией функций f и g, если 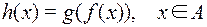(обозначение 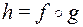). Часто говорят, что h получена подстановкой f в g.

Для многоместных функци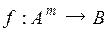й и 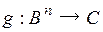возможны различные варианты подстановки f в g, задающие функции различных типов. Например, пр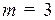и и 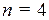функция 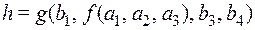имеет 6 аргументов и тип .

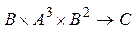Для множества многоместных функций типа 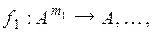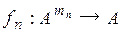возможны любые подстановки функций друг в друга, а также любые переименования аргументов. Например, переименование 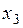в 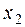из функции 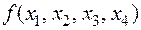четырёх аргументов порождает функцию трёх аргументов: .

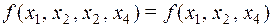Функция, полученная из функций 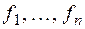некоторой подстановкой их друг в друга и переименованием аргументов, называется суперпозицией функций 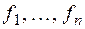. Выражение, задающее эту суперпозицию и содержащее функциональные знаки, скобки и символы аргументов, называется формулой.