Взаимно однозначные соответствия и мощность множеств

Утверждение (о взаимно однозначном соответствии равномощных множеств):Если между конечными множествами А и В существует взаимно однозначное соответствие, то .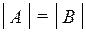

Этот факт:

1) позволяет установить равенство мощностей двух множеств, не вычисляя мощностей этих множеств;

2) дает возможность вычислить мощность множества, установив его взаимно однозначное соответствие с множеством, мощность которого известна или легко вычисляется.

Теорема (о числе подмножеств конечного множества)

Если для конечного множества А ( 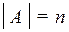), то число всех подмножеств множества А равно .

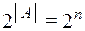Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие.

Счетные множества это множества равномощные N (т. е. между ними и N можно установить взаимно однозначное соответствие).

Утверждение 1: Множество 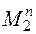– счетно.

Утверждение 2: Любое бесконечное подмножество множества N – счетно.

Утверждение 3: Множество 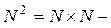– счетно.

Следствие: Множество 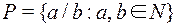– положительных рациональных чисел – счетно.

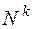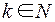Утверждение 4: Множество , где , - счетно.

Утверждение 5: Объединение конечного числа счетных множеств 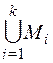– счетно.

Утверждение 6: Объединение счетного множества конечных множеств – счетно.

Следствие: Множество всех слов конечного алфавита – счетно.

Утверждение 7: Объединение счетного множества счетных множеств 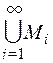– счетно.

Несчетные бесконечные множества называются множествами мощности континуум. (Мощность несчетного бесконечного множества называется континуумом).

Теорема (Кантора): Множество всех действительных чисел отрезка [0, 1] имеет мощность континуума.

Следствие: Множество всех подмножеств несчетного множества континуально.

Отношения

Подмножество 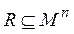называется n - местным отношением на множестве М. Говорят, что 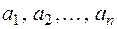находится в отношении R, если .

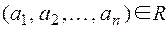Одноместное отношение – это просто подмножество М. Такие отношения называют признаками: элемент а – обладает признаком R, есл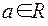и и .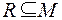

Свойства одноместных отношений это свойства подмножеств М, поэтому для случая n = 1 термин “отношение” употребляется редко.

Примером трехместного (тернарного) отношения является множество троек нападающих в хоккейной команде. Любой из нападающих находится в этом отношении со всеми теми игроками, с которыми он играет в одной тройке (один нападающий может, вообще говоря, участвовать более, чем в одной тройке).

При n = 2 – отношения называются двуместными или “бинарными”. Если a, b находятся в отношении R, это записывается aRb.

Пусть дано отношение R на М. Для любого подмножества 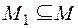естественно определяется отношение 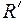, называемое сужением R на 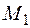, которое получается из R удалением всех пар, содержащих элементы, не принадлежащие 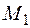. Иначе говоря, 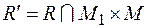. Строго говоря, R и 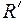- это разные отношения с разными областями определения.