Отношение эквивалентности

Отношение R на М называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из Е (т. е. любой единицы на диагонали матрицы Е) оно перестает быть рефлексивным и, следовательно, уже не является эквивалентным.

Пусть на множестве М задано отношение эквивалентности R. Осуществим построение классов эквивалентности, на которые разбивается множество М этим отношением.

Выберем элемент 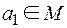и образуем класс (подмножество М) 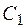, состоящий из 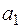и всех элементов, эквивалентных 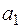; затем выберем элемент 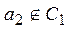, и образуем класс 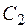, состоящий из 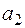и всех элементов, эквивалентных 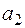и т. д. Получится система классов 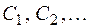(возможно бесконечная) такая, что любой элемент из М входит хотя бы в один класс, т. е. .

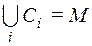Эта система обладает свойствами:

1) она образует разбиение, т. е. классы попарно не пересекаются;

2) любые два элемента из одного класса эквивалентны;

3) любые два элемента из разных классов неэквивалентны.

Мощность системы классов эквивалентности называется индексом разбиения.

С другой стороны, любое разбиение М на классы определяет некоторое отношение эквивалентности.

Отношение порядка

Отношение называется отношением нестрогогопорядка, если оно рефлексивно, антисимметрично, транзитивно.

Отношение называется отношением строгого порядка, если оно антирефлексивно, антисимметрично, транзитивно.

Оба типа таких отношений называются отношениями порядка.

Элементы a и b сравнимы по отношению порядка R, если выполняется aRb или bRa.

Множество М, на котором задано отношение порядка, называется полностью упорядоченным, если любые два элемента М сравнимы.

Множество М, на котором задано отношение порядка, называется частично упорядоченным, если не любые два элемента М сравнимы.