Лексико-графический порядок.
Пусть в списке букв конечного алфавита А порядок букв зафиксирован, т. е. всегда один и тот же, как, например, в русском и латинском алфавите. Тогда этот список определяет полное упорядочение букв, которое назовем отношением предшествования и обозначим “ 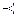 ”:
”: 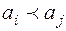 , если
, если 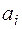 предшествует
предшествует 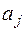 в списке букв).
в списке букв).
На основе отношения предшествования букв, строится отношение предшествования слов, определяемое следующим образом:
Пусть даны слова 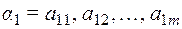 и
и 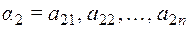 .
.
Тогда, 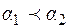 тогда и только тогда, когда
тогда и только тогда, когда
1) 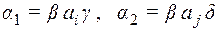 , где
, где 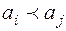 (
( 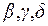 - слова возможно непустые,
- слова возможно непустые, 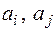 - буквы);
- буквы);
2) 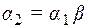 , где
, где 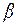 - непустое слово.
- непустое слово.
Это отношение задает полное упорядочение множества всех конечных слов в алфавите А, которое является лексикографическим упорядочением слов.
Операции и алгебры
N-арная операция на множестве М – это функция типа
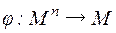 ,
,
где n – арность операции. Операция замкнута относительно множества М по определению, т. е. операция над элементами множества М, и результат тоже элемент М.
Алгеброй называется множество, вместе с заданной на нем совокупностью операций 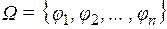 , т. е. система
, т. е. система
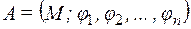 .
.
М – основное (несущее) множество (носитель алгебры) алгебры А.
Тип алгебры – вектор арностей операций.
Сигнатура – совокупность операций W.
Множество 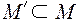 называется замкнутымотносительно n-арной операции
называется замкнутымотносительно n-арной операции 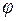 на М, если
на М, если
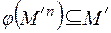 ,
,
т. е. если значения 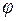 на аргументе из
на аргументе из 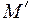 принадлежат
принадлежат 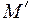 .
.
Если 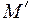 замкнуто относительно всех операций
замкнуто относительно всех операций 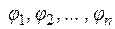 , алгебры М, то система
, алгебры М, то система
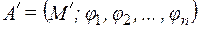
называется подалгеброй алгебры А (при этом 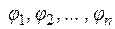 рассматриваются как операции на
рассматриваются как операции на 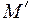 ).
).
Примеры:
1. Алгебра 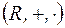 – называется полем действительных чисел.
– называется полем действительных чисел.
Обе операции бинарные, поэтому тип этой алгебры (2,2). Сигнатура 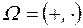 .
.
Подалгеброй этой алгебры является, например, поле рациональных чисел.
2. Пусть 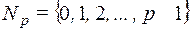 . Определим на
. Определим на 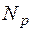 операции:
операции: 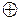 – «сложение по модулю р»,
– «сложение по модулю р», 
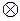 – «умножение по модулю р», следующим образом:
– «умножение по модулю р», следующим образом:
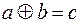 и
и 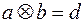 ,
,
где с и d – остатки от деления на р чисел а + b и а × b соответственно.
Пусть, например, р = 7, тогда 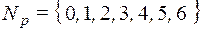 и
и
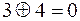 ,
, 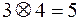 ,
, 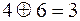 .
.
Часто обозначают: a + b = с (mod p) и a × b = d (mod p).
Конечным полем характеристики р называется алгебра 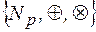 , если р – простое число.
, если р – простое число.
3. Пусть задано множество U.
Булеаном U называется множество всех подмножеств множества U (обозначается B(U)).
Булева алгебра множеств над U или алгебра Кантора – алгебра 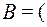 B(U),
B(U), 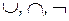 ). Ее тип (2,2,1), сигнатура
). Ее тип (2,2,1), сигнатура 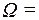 (
( 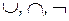 ).
).
Элементами основного множества булевой алгебры являются множества (подмножества U).
Для любого 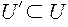
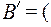 B(
B( 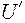 ),
), 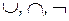 ) – является подалгеброй В.
) – является подалгеброй В.
Например, если 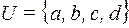 , то основное множество алгебры В содержит 16 элементов; алгебра
, то основное множество алгебры В содержит 16 элементов; алгебра 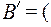 B(
B( 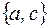 ),
), 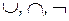 ) – подалгебра В. Ее несущее множество содержит четыре элемента.
) – подалгебра В. Ее несущее множество содержит четыре элемента.
Дата добавления: 2018-09-24; просмотров: 659;
