Полугруппы, группы, решетки
Алгебра с одной бинарной ассоциативной операцией называется полугруппой. Эта операция обычно называется умножением и обозначается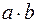 
или ab. Такая запись называется мультипликативной. В частности аа обозначается как 
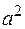, ааа как 
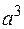и т. д. В общем случае 
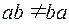. Полугруппа называется коммутативной, если операция умножения коммутативна. Если полугруппа содержит такой элемент е, что для любого а выполняется 
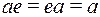, то такой элемент называется единицей. Полугруппа с единицей называется моноидом.
Пример 1.
Множество действительных чисел с операцией умножения является полугруппой с единицей. Здесь е = 1.
Утверждение 1.
Единица в полугруппе всегда единственна.
Группой называется полугруппа с единицей, в которой для каждого элемента а существует обратный элемент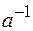 
, удовлетворяющий условию 
.
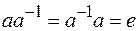Утверждение 2.
Для каждого элемента а в группе существует единственный обратный элемент .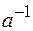
Число элементов группы называется порядком группы. Группа называется абелевой, если операция группы коммутативна. Группа, все элементы которой является степенями одного и того же элемента а, называется циклической.
Утверждение 3.
Циклическая группа всегда абелева.
Пример 2.
Множество целых чисел с операцией сложения является циклической.
Пример 3.
Множество целых чисел с операцией сложения является абелевой группой. Единицей по сложению является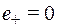 
. Для каждого числа 
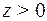существует обратный (здесь: противоположный) – z < 0. И наоборот. Для числа 0 противоположным является число 0.
Множество, на котором кроме операций заданы отношения называется алгебраической системой. Таким образом, алгебра является частным случаем алгебраической системы.
Рассмотрим частный случай алгебраической системы – решетку.
Пусть дано частично-упорядоченное множество М. Отношение порядка в общем случае будем обозначать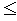 
. Верхней гранью элементов а и b из М называется элемент 
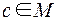, такой что 
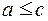и 
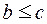. Нижней граньюэлементов а и b из М называется элемент 
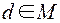, такой что 
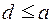и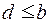 
. В общем случае для некоторых элементов а и b нижняя грань может не существовать или не быть единственной.
Решеткой называется частично упорядоченной множество, в котором для любых двух элементов а и b существует и единственна наибольшая нижняя грань, обозначаемая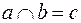 
и наименьшая верхняя грань, обозначаемая 
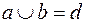. Таким образом решетка – это алгебраическая система вида 
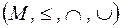с одним бинарным отношением и одной бинарной операцией.
Пример 4.
Любое полностью упорядоченное множество (например, множество целых чисел) можно превратить в решетку, определив для любых а и b из М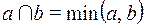 
; 
.
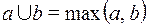Дата добавления: 2018-09-24; просмотров: 436;