Степени вершин графа

(Локальной) Степенью или (валентностью) 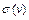вершины называется число ребер, инцидентных вершине v.

Если не оговаривается особо, то петля учитывается дважды при подсчете валентности вершины.

Граф называется правильным (с валентностью r) или r-валентным графом (регулярным, однородным), если степени всех его вершин равны.

Вершина называется изолированной, если она несмежна ни с одной из вершин графа, или, что то же самое, неинцидентна ни одному ребру. Степень этой вершины равна 0.

Вершина, имеющая степень, равную 1, называется висячей (концевой). Ребро, инцидентное висячей вершине, называют концевым.

Утверждение 1. (лемма о рукопожатиях): В н-графе сумма степеней всех вершин равна удвоенному числу ребер (т.е. четна): 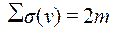, где m – число ребер.

Следствие 1. Произвольный граф имеет четное число вершин нечетной степени.

Следствие 1. Число ребер в полном графе равно , где n – число вершин.

В ор-графе две (локальных) степени вершины: 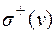и 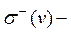число ребер с началом и концом в v соответственно.

Утверждение 2.Суммы степеней всех вершин ор-графа равны количеству ребер этого графа и, следовательно, равны между собой: 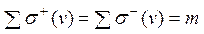, m – число ребер.