Операции над частями графа
Дополнение 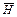 к части H определяется множеством всех ребер графа G, не принадлежащих H:
к части H определяется множеством всех ребер графа G, не принадлежащих H:
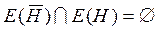 ,
, 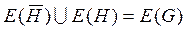 ;
;
Сумма 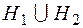 частей
частей 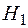 и
и 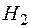 графа G, это граф, у которого
графа G, это граф, у которого
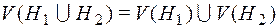 и
и 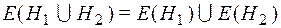 ;
;
Произведение 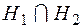 частей
частей 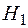 и
и 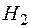 графа G, это граф, у которого
графа G, это граф, у которого
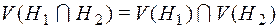 и
и 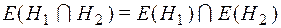 .
.
Части 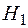 и
и 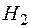 не пересекаются по вершинам, если они не имеют общих вершин, а значит и общих ребер:
не пересекаются по вершинам, если они не имеют общих вершин, а значит и общих ребер:
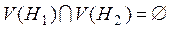 ,
, 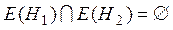 .
.
Части 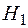 и
и 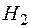 не пересекаются по ребрам, если
не пересекаются по ребрам, если
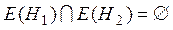 .
.
Если 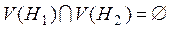 , то сумма
, то сумма 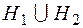 называется прямой.
называется прямой.
Графы и бинарные отношения
Отношению R, заданному на множестве V, взаимно однозначно соответствует ориентированный граф G(R) без кратных ребер с множеством вершин V, в котором ребро 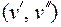 существует, только если выполнено
существует, только если выполнено 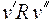 . Симметричному отношению R взаимно однозначно соответствует неориентированный граф без кратных ребер G(R). Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных ребер, не содержащий пар вершин с ребрами, противоположно направленными к разным вершинам. Если R рефлексивно, то граф G(R) без кратных ребер имеет петли во всех вершинах. Если R антирефлексивно, то граф G(R) без кратных ребер не имеет петель. Если R транзитивно, то в графе G(R) без кратных ребер для каждой пары ребер
. Симметричному отношению R взаимно однозначно соответствует неориентированный граф без кратных ребер G(R). Антисимметричному отношению R взаимно однозначно соответствует ориентированный граф без кратных ребер, не содержащий пар вершин с ребрами, противоположно направленными к разным вершинам. Если R рефлексивно, то граф G(R) без кратных ребер имеет петли во всех вершинах. Если R антирефлексивно, то граф G(R) без кратных ребер не имеет петель. Если R транзитивно, то в графе G(R) без кратных ребер для каждой пары ребер 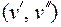 и
и 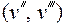 имеется замыкающее ребро
имеется замыкающее ребро 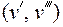 . Пусть
. Пусть 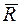 – дополнение отношения R на V:
– дополнение отношения R на V: 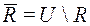 , где U –универсальное (полное) отношение
, где U –универсальное (полное) отношение 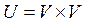 , т.е. отношение, имеющее место между любой парой элементов из V.
, т.е. отношение, имеющее место между любой парой элементов из V.
Граф G( 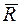 ) является дополнением графа G(R) (до полного орграфа K с множеством вершин V и множеством ребер
) является дополнением графа G(R) (до полного орграфа K с множеством вершин V и множеством ребер 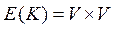 ).
).
Граф обратного отношения G( 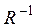 ) отличается от графа G(R) тем, что направления всех ребер заменены на обратные.
) отличается от графа G(R) тем, что направления всех ребер заменены на обратные.
Граф объединения двух отношений, заданных на V, 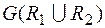 является графом суммы двух графов
является графом суммы двух графов 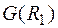 и
и 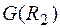 :
:
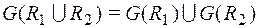 .
.
Граф пересечения отношений на V, 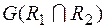 является графом пересечения двух графов
является графом пересечения двух графов 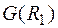 и
и 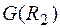 :
:
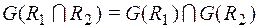 .
.
Дата добавления: 2018-09-24; просмотров: 1008;
