Свойства бинарных алгебраических операций
Условимся, чтобы последующие соотношения выглядели более привычно, результат применения бинарной операции 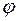 к элементам а и b записывать не в функциональном виде
к элементам а и b записывать не в функциональном виде 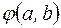 , а в виде
, а в виде 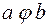 (как это принято в арифметических операциях).
(как это принято в арифметических операциях).
Операция 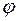 называется ассоциативной, если для любых элементов а, b, с
называется ассоциативной, если для любых элементов а, b, с
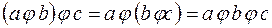 .
.
Выполнение условия ассоциативности означает, что скобки в выражении 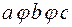 можно не расставлять.
можно не расставлять.
Пример:
1. Сложение и умножение чисел ассоциативны, что позволяет не ставить скобки в выражениях 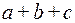 и
и 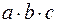 .
.
2. Возведение в степень 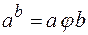 – не ассоциативна, так как
– не ассоциативна, так как
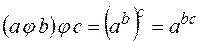 не равно
не равно 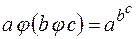 .
.
3. Композиция отображений – ассоциативная операция.
Операция 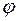 называется коммутативной, если для любых элементов a, b
называется коммутативной, если для любых элементов a, b
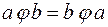 .
.
Пример:
1. Сложение чисел коммутативно («от перемены мест слагаемых сумма не меняется»): 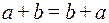 .
.
Умножение чисел коммутативно: 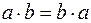 .
.
2. Вычитание и деление – некоммутативные операции.
Умножение матриц – некоммутативная операция, например:
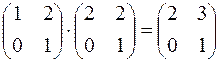 , но
, но 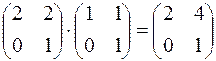 .
.
Операция 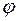 называется дистрибутивной слева относительно операции
называется дистрибутивной слева относительно операции 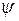 , если для любых a, b, с
, если для любых a, b, с
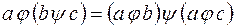 .
.
Операция 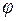 называется дистрибутивной справа относительно операции
называется дистрибутивной справа относительно операции 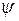 , если для любых a, b, с
, если для любых a, b, с
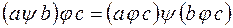 .
.
Дистрибутивность разрешает раскрыть скобки.
Примеры:
1. Умножение дистрибутивно относительно сложения слева и справа
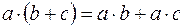 ;
; 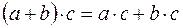 .
.
2. Возведение в степень дистрибутивно относительно умножения справа.
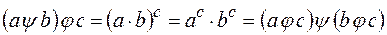 ,
,
но не слева, так как 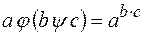 не равно
не равно
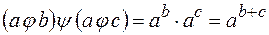 .
.
3. Сложение не дистрибутивно относительно умножения
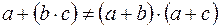 ,
,
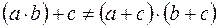 .
.
Дата добавления: 2018-09-24; просмотров: 1012;
