Свойства бинарных отношений
Отношение R на М называется рефлексивным, если для любого 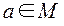 выполняется
выполняется 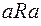 . Главная диагональ матрицы такого отношения содержит только единицы.
. Главная диагональ матрицы такого отношения содержит только единицы.
Отношение R на М называется антирефлексивным, если ни для какого 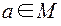
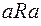 не выполняется. Главная диагональ матрицы отношения содержит только нули.
не выполняется. Главная диагональ матрицы отношения содержит только нули.
Отношение R на М называется симметричным, если для любой пары 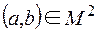 из aRb следует bRa (иначе говоря, для любой пары отношение R выполняется в обе стороны или не выполняется вообще). Матрица симметричного отношения – симметрична относительно главной диагонали:
из aRb следует bRa (иначе говоря, для любой пары отношение R выполняется в обе стороны или не выполняется вообще). Матрица симметричного отношения – симметрична относительно главной диагонали: 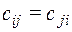 для всех i, j, т.е.
для всех i, j, т.е. 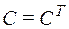
Отношение R на М называется антисимметричным, если из того, что (из aRb следует bRa) следует 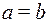 (т. е. ни для каких различных элементов множества М отношение R не выполняется). Матрица антисимметричного отношения не имеет ни одного симметричного относительно главной диагонали единичного элемента.
(т. е. ни для каких различных элементов множества М отношение R не выполняется). Матрица антисимметричного отношения не имеет ни одного симметричного относительно главной диагонали единичного элемента.
R симметрично тогда и только тогда, когда 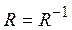 .
.
Отношение R на М называется транзитивным, если для любых a, b, c из множества М из того, что выполняется aRb иbRcследует, чтоaRc.
Для любого отношения R отношение 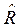 , называемое транзитивным замыканием R, определяется следующим образом:
, называемое транзитивным замыканием R, определяется следующим образом:
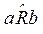 , если в М существует цепочка из n элементов
, если в М существует цепочка из n элементов 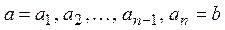 , в которой между соседними элементами выполнено отношение R:
, в которой между соседними элементами выполнено отношение R: 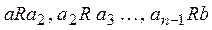
Если R – транзитивно, то по определению транзитивного замыкания: 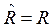 .
.
Дата добавления: 2018-09-24; просмотров: 663;
