Теорема (о мощности прямого произведения множеств).

Пусть 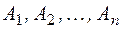- конечные множества и 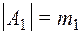, , 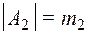... , 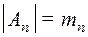. Тогда мощность множества 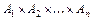равна произведению мощностей множеств :

.

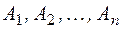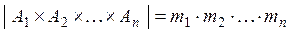Следствие: .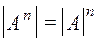

Эта теорема и ее следствие лежат в основе очень многих комбинаторных фактов.

Проекцией вектора длины n на i-ю ось называется его i-я координата (обозначение: ) .

Проекцией вектора 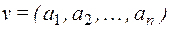на оси с номерами 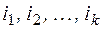называется вектор 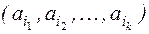длины k (обозначение: ).

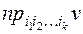Пусть V – множество векторов одинаковой длины.

Проекцией множества векторов V на i-ось называется множество проекций всех векторов из V на i-ось: (обозначение: .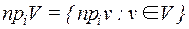

Проекция множества векторов V на оси с номерами :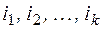

.

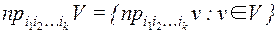В частности, если 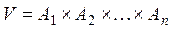, то = .

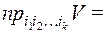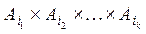В общем случае 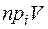- вовсе не обязательно прямое произведение, оно может быть и подмножеством.

Примеры:

1) Проекция точки плоскости на 1-ю ось – абсцисса, на 2-ю ось – ордината.

2) Дано множество векторов ;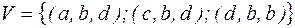

,

,

,

, ,

.

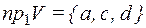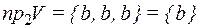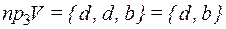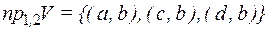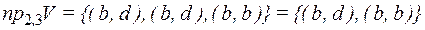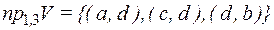3) 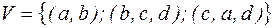. Чему равна 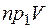? Ее найти нельзя, так как заданное множество V- множество векторов разной длины, в отношении которых никаких определений не было сделано.

Комбинаторика. Правило суммы