Множества и операции над ними
Множество можно представить как совокупность некоторых объектов, объединенных по какому-либо признаку.
Множество состоит из элементов. В зависимости от их числа множества различают как конечные или бесконечные. Конечные множества могут состоять из одного или нескольких элементов.
Мощность множества – количество его элементов.
Множество, не содержащее элементов, называется пустым множеством и обозначается Æ.
Множество обозначают заглавными буквами, а его элементы – прописными. Для записи множества используют фигурные скобки. Например, множество натуральных чисел от 3 до 10: М = {3, 4, 5, 6, 7, 8, 9, 10}.
Говоря об определенном множестве, мы полагаем, что для каждого объекта имеется две возможности: либо он входит в рассматриваемое множество, т.е. является его элементом, принадлежит ему (обозначается 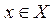 ); либо нет (обозначается
); либо нет (обозначается 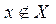 ).
).
Способы задания множества:
- перечисление всех элементов множества, например, множество однозначных неотрицательных чисел X = {0, 1, 2, 3, …, 9};
- указание общего свойства, которым обладают все элементы множества, например, множество четных натуральных чисел X = {2, 4, 6, 8, 10, 12, …} или X = {x: x = 2n, 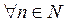 };
};
- рекуррентно, например: 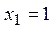 ,
, 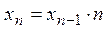 и др.
и др.
Множество А называют подмножеством множества В (обозначается 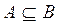 ), если каждый элемент множества А является также элементом множества В.
), если каждый элемент множества А является также элементом множества В.
Множества А и В называют равными ( 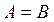 ), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если
), если каждый элемент множества А является одновременно элементом множества В и наоборот, т.е. если 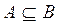 и
и 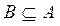 . Другими словами, два множества равны, если они состоят из одних и тех же элементов.
. Другими словами, два множества равны, если они состоят из одних и тех же элементов.
Множество I называется универсальным множеством (множество всех подмножеств) для некоторой системы множеств, если каждое множество этой системы является подмножеством I, т.е. {A, B, C, …}: 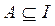 ,
, 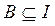 ,
, 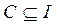 , …
, …
Дополнением множества А ( 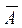 ) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
) называется множество, состоящее из тех и только тех элементов универсального множества, которые не входят в множество А.
Объединением двух множеств А и В ( 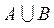 ) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
) называется множество С, состоящее из тех элементов, которые принадлежат или множеству А, или В, или А и В одновременно.
Пересечением двух множеств А и В ( 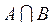 ) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
) называется множество С, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Разностью двух множеств А и В ( 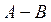 или
или 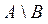 ) называется множество тех элементов множества А , которые не принадлежат множеству В:
) называется множество тех элементов множества А , которые не принадлежат множеству В:
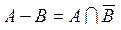 .
.
Прямым (декартовым) произведением двух множеств А и В ( 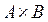 ) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Пример. Заданы два множества: А = {-2, -1, 0, 1, 2} и B = {0, 2, 4, 5}. Определить множества 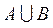 ;
; 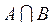 ;
; 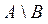 ;
; 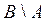 ;
; 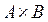 ;
; 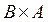 и их мощность.
и их мощность.
Множество А = {-2, -1, 0, 1, 2} состоит из пяти элементов, следовательно мощность этого множества равна 5: 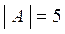 .
.
Аналогично, B = {0, 2, 4, 5} содержит четыре элемента: 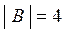 .
.
По определению пересечение двух множеств состоит только из общих для обоих множеств элементов, следовательно, 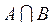 = {0, 2} и
= {0, 2} и 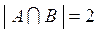 .
.
По определению объединение двух множеств состоит из всех элементов, которые принадлежат и множеству А, и множеству В, следовательно, 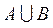 = {-2, -1, 0, 1, 2, 4, 5} и
= {-2, -1, 0, 1, 2, 4, 5} и 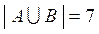 .
.
Множество 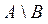 является разностьюдвух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно
является разностьюдвух множеств А и В и состоит из элементов множества А, которые одновременно не принадлежат множеству В, следовательно 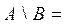
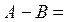 {-2, -1, 1} и
{-2, -1, 1} и 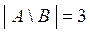 .
.
Аналогично, 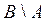
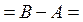 {4, 5} и
{4, 5} и 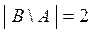 .
.
Прямое (декартово) произведение:
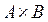 = {(-2, 0); (-2, 2); (-2, 4); (-2, 5); (-1, 0); (-1, 2); (-1, 4); (-1, 5); (0, 0); (0, 2); (0, 4); (0, 5); (1, 0); (1, 2); (1, 4); (1, 5); (2, 0); (2, 2); (2, 4); (2, 5)}
= {(-2, 0); (-2, 2); (-2, 4); (-2, 5); (-1, 0); (-1, 2); (-1, 4); (-1, 5); (0, 0); (0, 2); (0, 4); (0, 5); (1, 0); (1, 2); (1, 4); (1, 5); (2, 0); (2, 2); (2, 4); (2, 5)}
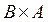 = {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
= {(0, -2); (0, -1); (0, 0); (0, 1); (0, 2); (2, -2); (2, -1); (2, 0); (2, 1); (2, 2); (4, -2); (4, -1); (4, 0); (4, 1); (4, 2); (5, -2); (5, -1); (5, 0); (5, 1); (5, 2)}
Из этого примера видно, что 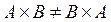 , но при этом
, но при этом 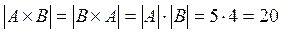 .
.
Дата добавления: 2018-09-24; просмотров: 1255;
